题目内容
在△ABC中,AB=AC=13,BC=10,则△ABC的面积为( )
| A、30 | B、60 | C、65 | D、120 |
考点:勾股定理,等腰三角形的性质
专题:
分析:作底边上的高,构造直角三角形.运用等腰三角形的性质及三角形的面积公式求解.
解答: 解:如图,作AD⊥BC于点D,则BD=
解:如图,作AD⊥BC于点D,则BD=
BC=5.
在Rt△ABD,
∵AD2=AB2-BD2,
∴AD=
=12,
∴△ABC的面积=
BC•AD=
×10×12=60.
故选B.
 解:如图,作AD⊥BC于点D,则BD=
解:如图,作AD⊥BC于点D,则BD=| 1 |
| 2 |
在Rt△ABD,
∵AD2=AB2-BD2,
∴AD=
| 132-52 |
∴△ABC的面积=
| 1 |
| 2 |
| 1 |
| 2 |
故选B.
点评:本题考查了勾股定理,等腰三角形的性质和三角形的面积,难度适中.

练习册系列答案
相关题目
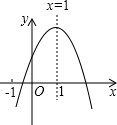 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列4个结论中:①abc>0;②b<a+c;③4a+2b+c>0;④b2-4ac>0;⑤b=2a.正确的是
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列4个结论中:①abc>0;②b<a+c;③4a+2b+c>0;④b2-4ac>0;⑤b=2a.正确的是 如图,A、B两点在数轴上对应的数分别是-20、24,点P、Q两点同时出发,在数轴上运动,它们的速度分别是2个单位/秒、4个单位/秒,它们运动的时间为t秒,当点P、Q在A、B之间相向运动,且满足OP=OQ,则点P对应的数是
如图,A、B两点在数轴上对应的数分别是-20、24,点P、Q两点同时出发,在数轴上运动,它们的速度分别是2个单位/秒、4个单位/秒,它们运动的时间为t秒,当点P、Q在A、B之间相向运动,且满足OP=OQ,则点P对应的数是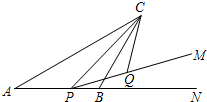 如图,△ABC中,AC=10,∠BAC=30°,点P是射线AB上的一个动点,cos∠CPM=
如图,△ABC中,AC=10,∠BAC=30°,点P是射线AB上的一个动点,cos∠CPM=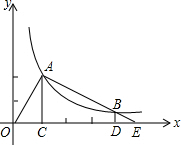 如图,A是反比例函数y=
如图,A是反比例函数y= 已知点P为⊙O所在平面上一点,过点P的两条直线PA,PC分别交⊙O于A,B和C,D两点,且PO平分∠APC.求证:PA=PC.
已知点P为⊙O所在平面上一点,过点P的两条直线PA,PC分别交⊙O于A,B和C,D两点,且PO平分∠APC.求证:PA=PC.