题目内容
16.当我们利用两种不同的方法计算同一图形的面积时,可以得到一个等式,例如,由图1,可得等式:(a+2b)(a+b)=a2+3ab+2b2.
(1)由图2,可得等式:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc.
(2)利用(1)中所得到的结论,解决下面的问题:
已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
(3)如图3,琪琪用2张A型纸片,3张B型纸片,5张C型纸片拼出一个长方形,那么该长方形较长的一条边长为2a+3b.(直接写出答案)
分析 (1)根据图2,利用直接求与间接法分别表示出正方形面积,即可确定出所求等式;
(2)根据(1)中结果,求出所求式子的值即可;
(3)根据题意列出关系式,即可确定出长方形较长的边.
解答 解:(1)(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;
(2)∵a+b+c=11,ab+bc+ac=38,
∴a2+b2+c2=(a+b+c)2-2(ab+ac+bc)=121-76=45;
(3)根据题意得:2a2+5ab+3b2=(2a+3b)(a+b),
则较长的一边为2a+3b.
故答案为:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;2a+3b.
点评 此题考查了多项式乘以多项式,熟练掌握运算法则是解本题的关键.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
5. 如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP、CP分别平分∠EDC、∠BCD、则∠P=( )
如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP、CP分别平分∠EDC、∠BCD、则∠P=( )
 如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP、CP分别平分∠EDC、∠BCD、则∠P=( )
如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP、CP分别平分∠EDC、∠BCD、则∠P=( )| A. | 65° | B. | 60° | C. | 55° | D. | 50° |
6.如图,某数学小组在课外实践活动中,用电钻将四个质地均匀、质量相等的木质小正方体,分别从不同方向钻一个直径一样的直圆孔,再用天平分别称得下列小正方体的质量,下列说法中正确的是( )
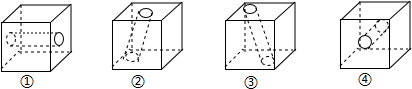

| A. | ①和④更重 | B. | ③最轻 | C. | 质量仍然一样 | D. | ②和③更重 |
 在如图所示的平面直角坐标系中,将坐标是(1,0),(0,4),(2,4),(4,4),(3,0),的点用线段依次连接起来形成一个图案.
在如图所示的平面直角坐标系中,将坐标是(1,0),(0,4),(2,4),(4,4),(3,0),的点用线段依次连接起来形成一个图案.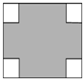 如图所示,在一个边长为12cm的正方形的四个角都剪去一个大小相等的小正方形,当小正方形的边长由小到大变化时,图中阴影部分的面积也随之发生变化.
如图所示,在一个边长为12cm的正方形的四个角都剪去一个大小相等的小正方形,当小正方形的边长由小到大变化时,图中阴影部分的面积也随之发生变化.