题目内容
9. 已知△ABO在平面直角坐标系中的位置如图所示,请在图上完成下列操作并解答问题:
已知△ABO在平面直角坐标系中的位置如图所示,请在图上完成下列操作并解答问题:(1)作△OAB关于y轴对称的△OA'B'(其中点A、B分别对应点A'、B'),并写出点A'和B'的坐标;
(2)确定直线A'B'的表达式.
分析 (1)根据轴对称的性质进行作图即可;
(2)根据待定系数法求得直线A'B'的表达式.
解答 解:(1)如图所示,△OA'B'即为所求,
由图可得,点A'和B'的坐标分别为(1,4),(4,1);
(2)设直线A'B'的表达式为y=kx+b,
∵点A'和B'的坐标分别为(1,4),(4,1),
∴$\left\{\begin{array}{l}{4=k+b}\\{1=4k+b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-1}\\{b=5}\end{array}\right.$,
∴直线A'B'的表达式为y=-x+5.
点评 本题主要考查了运用轴对称变换进行作图以及待定系数法求一次函数解析式的运用,解决问题时注意:画一个图形的轴对称图形时,先从确定一些特殊的对称点开始.

练习册系列答案
相关题目
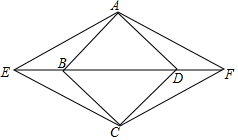 已知:如图,在菱形ABCD中,E、F分别在射线DB和射线BD上,且BE=DF.
已知:如图,在菱形ABCD中,E、F分别在射线DB和射线BD上,且BE=DF. 如图,△ABC中,已知MN∥BC分别交AB、AC于点M、N,DN∥MC交AB于点D.
如图,△ABC中,已知MN∥BC分别交AB、AC于点M、N,DN∥MC交AB于点D. 如图,在△ABC中,D、E、F分别是边AB,AC,BC上的点,且DE∥BC,EF∥AB,AD:DB=3:2,BC=20cm,求FC的长.
如图,在△ABC中,D、E、F分别是边AB,AC,BC上的点,且DE∥BC,EF∥AB,AD:DB=3:2,BC=20cm,求FC的长.