题目内容
17．
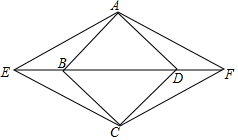已知：如图，在菱形ABCD中，E、F分别在射线DB和射线BD上，且BE=DF．求证：四边形AECF是菱形．
分析 由菱形的性质得出OD=OB，OA=OC，BD⊥AC，证出OE=OF，得出四边形AECF是平行四边形，再由AC⊥BD，即可得出四边形AECF是菱形．
解答 证明：连接AC，交BD于O，如图所示：
∵四边形ABCD是菱形，
∴OD=OB，OA=OC，BD⊥AC，
∵BE=DF，
∴OB+BE=OD+DF，
即OE=OF，
∴四边形AECF是平行四边形，
又∵AC⊥BD，
∴四边形AECF是菱形．
点评 本题考查了菱形对角线互相垂直平分的性质与判定、平行四边形的判定；证明四边形AECF是平行四边形是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
7．下列各式中，属于二次根式的有（ ）
①$\sqrt{15}$；②$\sqrt{\frac{1}{a}}$；③$\sqrt{{a}^{2}+{b}^{2}}$；④$\sqrt{{a}^{2}b}$；⑤$\sqrt{2ab×3bc}$；⑥$\sqrt{5\frac{1}{2}}$．
①$\sqrt{15}$；②$\sqrt{\frac{1}{a}}$；③$\sqrt{{a}^{2}+{b}^{2}}$；④$\sqrt{{a}^{2}b}$；⑤$\sqrt{2ab×3bc}$；⑥$\sqrt{5\frac{1}{2}}$．
| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
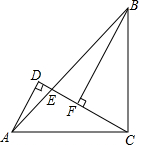如图所示，△ADC是直角三角形，∠ADC=90°，AC=BC，且AC⊥BC于点C，BF⊥CD于F，连接AB交CD于E，试说明：AD+DF=BF．
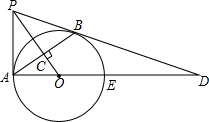如图，PB为⊙O的切线，B为切点，过B作OP的垂线BA，垂足为C，交⊙O于点A，连接PA、AO，并延长AO交⊙O于点E，与PB的延长线交于点D．
已知△ABO在平面直角坐标系中的位置如图所示，请在图上完成下列操作并解答问题：
6．二次函数y1=a（x-x1）（x-x2）（a≠0，x1≠x2）的图象与一次函数y2=bx+c（b≠0）的图象交于点（x1，0），若函数y=y1-2y2的图象经过点（x2，1），则有（ ）
| A． | 2b（x1-x2）=1 | B． | 2b（x2-x1）=1 | C． | b（x1-x2）=2 | D． | b（x2-x1）=2 |
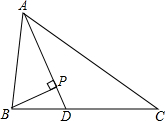如图，△ABC中，AD平分∠BAC，BP⊥AD于点P，AB=5，BP=1，AC=9，说明∠ABP=2∠ACB的理由．