题目内容
1. 如图,在△ABC中,D、E、F分别是边AB,AC,BC上的点,且DE∥BC,EF∥AB,AD:DB=3:2,BC=20cm,求FC的长.
如图,在△ABC中,D、E、F分别是边AB,AC,BC上的点,且DE∥BC,EF∥AB,AD:DB=3:2,BC=20cm,求FC的长.
分析 根据平行线分线段成比例定理得到$\frac{AE}{EC}$=$\frac{AD}{DB}$=$\frac{3}{2}$,$\frac{BF}{FC}$=$\frac{AE}{EC}$=$\frac{3}{2}$,计算即可.
解答 解:∵DE∥BC,
∴$\frac{AE}{EC}$=$\frac{AD}{DB}$=$\frac{3}{2}$,
∵EF∥AB,
∴$\frac{BF}{FC}$=$\frac{AE}{EC}$=$\frac{3}{2}$,又BC=20cm,
∴FC=8cm.
点评 本题考查的是平行线分线段成比例定理,灵活运用定理、找准对应关系是解题的关键.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
11.(π-3)0+2-2=( )
| A. | 5 | B. | 1$\frac{1}{4}$ | C. | -3 | D. | -1$\frac{1}{4}$ |
6.二次函数y1=a(x-x1)(x-x2)(a≠0,x1≠x2)的图象与一次函数y2=bx+c(b≠0)的图象交于点(x1,0),若函数y=y1-2y2的图象经过点(x2,1),则有( )
| A. | 2b(x1-x2)=1 | B. | 2b(x2-x1)=1 | C. | b(x1-x2)=2 | D. | b(x2-x1)=2 |
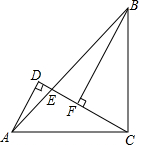 如图所示,△ADC是直角三角形,∠ADC=90°,AC=BC,且AC⊥BC于点C,BF⊥CD于F,连接AB交CD于E,试说明:AD+DF=BF.
如图所示,△ADC是直角三角形,∠ADC=90°,AC=BC,且AC⊥BC于点C,BF⊥CD于F,连接AB交CD于E,试说明:AD+DF=BF. 已知△ABO在平面直角坐标系中的位置如图所示,请在图上完成下列操作并解答问题:
已知△ABO在平面直角坐标系中的位置如图所示,请在图上完成下列操作并解答问题: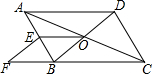 如图,在?ABCD中,对角线AC,BD交于点O,E为AB中点,点F在CB的延长线上,且EF∥BD.
如图,在?ABCD中,对角线AC,BD交于点O,E为AB中点,点F在CB的延长线上,且EF∥BD.