题目内容
15.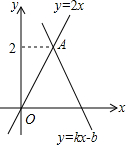 如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A,则不等式0<kx+b<2x的解集为( )
如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A,则不等式0<kx+b<2x的解集为( )| A. | 1<x<2 | B. | x>2 | C. | x>0 | D. | 0<x<1 |
分析 先利用正比例函数解析式确定A点坐标,然后观察函数图象得到,当x>1时,直线y=2x都在直线y=kx+b的上方,当x<2时,直线y=kx+b在x轴上方,于是可得到不等式0<kx+b<2x的解集.
解答 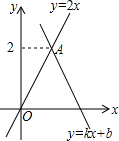 解:设A点坐标为(x,2),
解:设A点坐标为(x,2),
把A(x,2)代入y=2x,
得2x=2,解得x=1,
则A点坐标为(1,2),
所以当x>1时,2x>kx+b,
∵函数y=kx+b(k≠0)的图象经过点B(2,0),
∴x<2时,kx+b>0,
∴不等式0<kx+b<2x的解集为1<x<2.
故选A.
点评 本题考查了一次函数与一元一次不等式的关系:从函数的角度看,就是寻求使一次函数y=ax+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
7.如图是本地区一种产品30天的销售图象,图①是产品日销售量y(单位:件)与时间t(单位;天)的函数关系,图②是一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润,下列结论错误的是( )
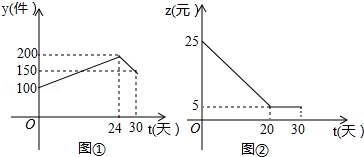

| A. | 第24天的销售量最多 | |
| B. | 20≤t≤30日销售利润不变 | |
| C. | 第30天的日销售利润是750元 | |
| D. | 当0≤t≤24时,设产品日销售量y与时间t的函数关系为y=$\frac{25}{6}$t+100 |
4.代数式2016-a2+2ab-b2的最大值是( )
| A. | 2015 | B. | 2016 | C. | 2017 | D. | 不存在 |
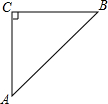 如图,等腰直角△ABC中,AC=BC=$\sqrt{5}$,等腰直角△CDP中,且PB=$\sqrt{2}$.∠CPB=135°,将△CDP绕点C旋转,求BD的长.
如图,等腰直角△ABC中,AC=BC=$\sqrt{5}$,等腰直角△CDP中,且PB=$\sqrt{2}$.∠CPB=135°,将△CDP绕点C旋转,求BD的长.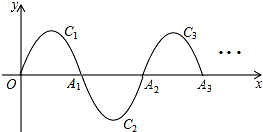 如图,一段抛物线y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x 轴于点A2;将C2绕点A2旋转180°得C3,交x 轴于点A3;…如此进行下去,得到一条“波浪线”.若点P(35,m)在此“波浪线”上,则m的值为-2.
如图,一段抛物线y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x 轴于点A2;将C2绕点A2旋转180°得C3,交x 轴于点A3;…如此进行下去,得到一条“波浪线”.若点P(35,m)在此“波浪线”上,则m的值为-2.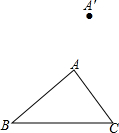 平移三角形ABC,使点A移动到点A′,画出平移后的△A′B′C′.若AB=3cm,则A′B′=3cm;若∠C′=45°,则∠C=45°.
平移三角形ABC,使点A移动到点A′,画出平移后的△A′B′C′.若AB=3cm,则A′B′=3cm;若∠C′=45°,则∠C=45°.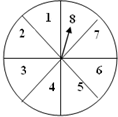 自由转动如图所示的转盘.下列事件中哪些是必然事件?那些是随机事件?根据你的经验,将这些事件的序号按发生的可能性从小到大的顺序排列.
自由转动如图所示的转盘.下列事件中哪些是必然事件?那些是随机事件?根据你的经验,将这些事件的序号按发生的可能性从小到大的顺序排列.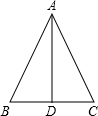 如图,在△ABC中,AB=AC=10cm,BC=12cm,AD⊥BC于点D,则AD=8cm.
如图,在△ABC中,AB=AC=10cm,BC=12cm,AD⊥BC于点D,则AD=8cm.