题目内容
6.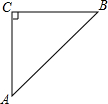 如图,等腰直角△ABC中,AC=BC=$\sqrt{5}$,等腰直角△CDP中,且PB=$\sqrt{2}$.∠CPB=135°,将△CDP绕点C旋转,求BD的长.
如图,等腰直角△ABC中,AC=BC=$\sqrt{5}$,等腰直角△CDP中,且PB=$\sqrt{2}$.∠CPB=135°,将△CDP绕点C旋转,求BD的长.
分析 根据SAS证明△ACD≌△BCP,得出AD=BP=$\sqrt{2}$,∠ADC=∠BPC=135°.再分两种情况进行讨论:①如图1,证明A、D、P三点共线,△ABP是直角三角形,进而利用勾股定理求解;②如图2,证明B、P、D三点共线,△ABD是直角三角形,进而利用勾股定理求解.
解答 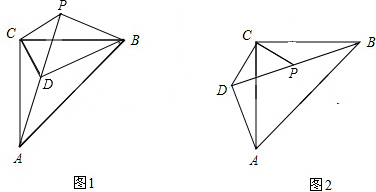 解:∵∠ACB=90°,∠DCP=90°,
解:∵∠ACB=90°,∠DCP=90°,
∴∠ACD=∠BCP.
在△ACD与△BCP中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCP}\\{CD=CP}\end{array}\right.$,
∴△ACD≌△BCP(SAS),
∴AD=BP=$\sqrt{2}$,∠ADC=∠BPC=135°.
①如图1,∵△CDP是等腰直角三角形,
∴∠CPD=∠CDP=45°,
∴∠APB=∠CPB-∠CPD=90°,
∠CDP+∠ADC=45°+135°=180°,
∴A、D、P三点共线,△ABP是直角三角形.
∵等腰直角△ABC中,AC=BC=$\sqrt{5}$,
∴AB=$\sqrt{2}$AC=$\sqrt{10}$,
∵△ABP中,∠APB=90°,PB=$\sqrt{2}$,
∴AP=$\sqrt{A{B}^{2}-B{P}^{2}}$=$\sqrt{10-2}$=2$\sqrt{2}$,
∴DP=AP-AD=2$\sqrt{2}$-$\sqrt{2}$=$\sqrt{2}$,
∴BD=$\sqrt{B{P}^{2}+D{P}^{2}}$=$\sqrt{2+2}$=2;
②如图2,同(1)可得B、P、D三点共线,△ABD是直角三角形,
则BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=$\sqrt{10-2}$=2$\sqrt{2}$.
综上所述,BD的长为2或2$\sqrt{2}$.
点评 本题考查了全等三角形的判定与性质,等腰直角三角形的性质,勾股定理,证明三点共线以及正确分类是解题的关键.

 一本好题口算题卡系列答案
一本好题口算题卡系列答案| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
| A. | 两个锐角的和为直角 | B. | 两个锐角的和为钝角 | ||
| C. | 两个锐角的和为锐角 | D. | 互余且非零度的两个角都是锐角 |
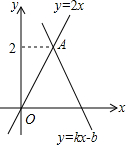 如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A,则不等式0<kx+b<2x的解集为( )
如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A,则不等式0<kx+b<2x的解集为( )| A. | 1<x<2 | B. | x>2 | C. | x>0 | D. | 0<x<1 |
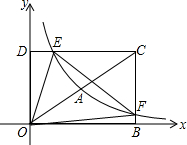 如图,在平面直角坐标系xOy中,矩形OBCD的顶点B,D的坐标分别为(8,0),(0,4).若反比例函数y=$\frac{{k}_{1}}{x}$(x>0)的图象经过对角线OC的中点A,分别交DC边于点E,交BC边于点F.设直线EF的函数表达式为y=k2x+b.
如图,在平面直角坐标系xOy中,矩形OBCD的顶点B,D的坐标分别为(8,0),(0,4).若反比例函数y=$\frac{{k}_{1}}{x}$(x>0)的图象经过对角线OC的中点A,分别交DC边于点E,交BC边于点F.设直线EF的函数表达式为y=k2x+b.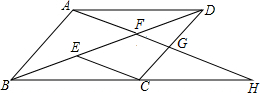 如图,在四边形ABCD中,AB∥DC,E、F为对角线BD上两点,且BE=DF,AF∥EC.
如图,在四边形ABCD中,AB∥DC,E、F为对角线BD上两点,且BE=DF,AF∥EC. 如图所示,选择点O为对称中心,画出与△ABC关于点O对称的△A1B1C1.
如图所示,选择点O为对称中心,画出与△ABC关于点O对称的△A1B1C1.