题目内容
14.计算(1)$\sqrt{(-7)^{2}}$=7,(2)±$\sqrt{2\frac{7}{9}}$=±$\frac{5}{3}$,(3)$\root{3}{-125}$=-5.分析 原式利用二次根式性质,平方根,立方根定义计算即可得到结果.
解答 解:(1)原式=|-7|=7;
(2)原式=±$\frac{5}{3}$;
(3)原式=-5.
故答案为:(1)7;(2)±$\frac{5}{3}$;(3)-5.
点评 此题考查了立方根,平方根,以及算术平方根,熟练掌握各自的定义是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.已知关于x,y的方程组$\left\{{\begin{array}{l}{ax+by=10}\\{mx-ny=8}\end{array}}\right.$的解是$\left\{{\begin{array}{l}{x=1}\\{y=2}\end{array}}\right.$,则关于x,y的方程组$\left\{{\begin{array}{l}{\frac{1}{2}a(x+y)+\frac{1}{3}b(x-y)=10}\\{\frac{1}{2}m(x+y)-\frac{1}{3}n(x-y)=8}\end{array}}\right.$的解为( )
| A. | $\left\{{\begin{array}{l}{x=1}\\{y=2}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{x=2}\\{y=1}\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}{x=4}\\{y=-2}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{x=3}\\{y=2}\end{array}}\right.$ |
5.长度为1cm、2cm、3cm、4cm、5cm的五条线段,若以其中的三条线段为边构成三角形,可以构成不同的三角形共有( )
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
15.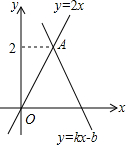 如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A,则不等式0<kx+b<2x的解集为( )
如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A,则不等式0<kx+b<2x的解集为( )
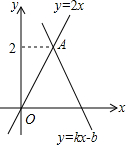 如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A,则不等式0<kx+b<2x的解集为( )
如图,函数y=kx+b(k≠0)的图象经过点B(2,0),与函数y=2x的图象交于点A,则不等式0<kx+b<2x的解集为( )| A. | 1<x<2 | B. | x>2 | C. | x>0 | D. | 0<x<1 |

 如图,点A、C、F、B在同一直线上,CD平分∠ECB,FG∥CD.若∠ECA=58°,则∠GFB的大小为61°.
如图,点A、C、F、B在同一直线上,CD平分∠ECB,FG∥CD.若∠ECA=58°,则∠GFB的大小为61°.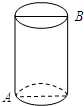 如图所示,有一个圆柱体,高为12cm,底面半径为3cm,在圆柱下底面A处有一只蜘蛛.它想到上底面B处捉住一只苍蝇,则蜘蛛所走的最短路线长应为多少cm(π取3.0).
如图所示,有一个圆柱体,高为12cm,底面半径为3cm,在圆柱下底面A处有一只蜘蛛.它想到上底面B处捉住一只苍蝇,则蜘蛛所走的最短路线长应为多少cm(π取3.0).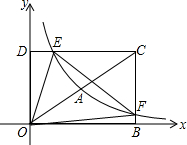 如图,在平面直角坐标系xOy中,矩形OBCD的顶点B,D的坐标分别为(8,0),(0,4).若反比例函数y=$\frac{{k}_{1}}{x}$(x>0)的图象经过对角线OC的中点A,分别交DC边于点E,交BC边于点F.设直线EF的函数表达式为y=k2x+b.
如图,在平面直角坐标系xOy中,矩形OBCD的顶点B,D的坐标分别为(8,0),(0,4).若反比例函数y=$\frac{{k}_{1}}{x}$(x>0)的图象经过对角线OC的中点A,分别交DC边于点E,交BC边于点F.设直线EF的函数表达式为y=k2x+b.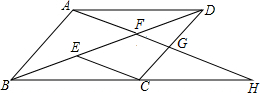 如图,在四边形ABCD中,AB∥DC,E、F为对角线BD上两点,且BE=DF,AF∥EC.
如图,在四边形ABCD中,AB∥DC,E、F为对角线BD上两点,且BE=DF,AF∥EC.