题目内容
19.已知O是矩形ABCD的对角线的交点,AB=6,BC=8,则点O到AB、BC的距离分别是( )| A. | 3、5 | B. | 4、5 | C. | 3、4 | D. | 4、3 |
分析 作OM⊥AB于M,ON⊥BC于N,由矩形的性质得出OA=OB=OC=OD,由等腰三角形的性质得出AM=BM,BN=CN,证出OM、ON是△ABC的中位线,由三角形中位线定理得出OM=$\frac{1}{2}$BC=4,ON=$\frac{1}{2}$AB=3即可.
解答 解:作OM⊥AB于M,ON⊥BC于N,如图所示: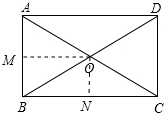
∵四边形ABCD是矩形,
∴OA=OC,OB=OD,AC=BD,
∴OA=OB=OC=OD,
∵OM⊥AB于M,ON⊥BC于N,
∴AM=BM,BN=CN,
∴OM、ON是△ABC的中位线,
∴OM=$\frac{1}{2}$BC=4,ON=$\frac{1}{2}$AB=3;
故选:D.
点评 本题考查了矩形的性质、三角形中位线定理、等腰三角形的性质;熟练掌握矩形的性质,由三角形中位线定理得出结果是解决问题的关键.

练习册系列答案
相关题目
9.下列方程中,属于一元二次方程的是( )
| A. | $\frac{1}{{x}^{2}}+\frac{1}{x}-3=0$ | B. | ax2+bx+c=0 | C. | x2+5x=x2-3 | D. | x2-3x+2=0 |
 如图,矩形OABC的顶点A、C的坐标分别为(0,10)、(4,0),反比例函数y=$\frac{k}{x}(k≠0)$在第一象限内的图象过矩形OABC的对角线的交点M,并与AB、BC分别交于点E、F,连接OE、EF、OF,则△OEF的面积为$\frac{75}{4}$.
如图,矩形OABC的顶点A、C的坐标分别为(0,10)、(4,0),反比例函数y=$\frac{k}{x}(k≠0)$在第一象限内的图象过矩形OABC的对角线的交点M,并与AB、BC分别交于点E、F,连接OE、EF、OF,则△OEF的面积为$\frac{75}{4}$.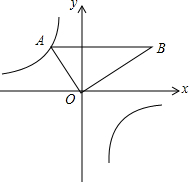 如图,把含30°角的三角板放置在如图所示的平面直角坐标系中,∠AOB=90°,∠B=30°,OA=2,斜边AB∥x轴,点A在双曲线上.
如图,把含30°角的三角板放置在如图所示的平面直角坐标系中,∠AOB=90°,∠B=30°,OA=2,斜边AB∥x轴,点A在双曲线上. 如图,三个全等的小矩形沿“横-竖-横”排列在一个边长分别为5.7,4.5的大矩形中,图中一个小矩形的周长等于6.8.
如图,三个全等的小矩形沿“横-竖-横”排列在一个边长分别为5.7,4.5的大矩形中,图中一个小矩形的周长等于6.8.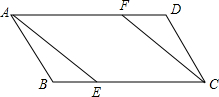 如图,在?ABCD中,已知点E、F分别在边BC和AD上,且BE=DF.求证:AE=CF.
如图,在?ABCD中,已知点E、F分别在边BC和AD上,且BE=DF.求证:AE=CF.