题目内容
8.已知矩形的对角线的夹角为60°,对角线长为6cm,则矩形ABCD的周长为6+6$\sqrt{3}$cm.分析 根据矩形的对角线相等且互相平分可得OA=OB,从而判断出△AOB是等边三角形,根据等边三角形的性质可得AB=OA,再利用勾股定理列式求出BC,即可得出结果.
解答 解:如图, ∵矩形的对角线的长为6,
∵矩形的对角线的长为6,
∴OA=OB=$\frac{1}{2}$×6cm=3cm,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴AB=OA=3cm,
在Rt△ABC中,BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$,
∴矩形ABCD的周长=2(3+3$\sqrt{3}$)=6+6$\sqrt{3}$(cm);
故答案为:6+6$\sqrt{3}$cm.
点评 本题考查了矩形的性质,等边三角形的判定与性质,熟记矩形的对角线相等且互相平分是解题的关键,作出图形更形象直观.

练习册系列答案
相关题目
18.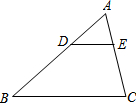 如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,若DE=2,BC=5,则AD:DB=( )
如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,若DE=2,BC=5,则AD:DB=( )
 如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,若DE=2,BC=5,则AD:DB=( )
如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,若DE=2,BC=5,则AD:DB=( )| A. | 3:2 | B. | 3:5 | C. | 2:5 | D. | 2:3 |
19.已知O是矩形ABCD的对角线的交点,AB=6,BC=8,则点O到AB、BC的距离分别是( )
| A. | 3、5 | B. | 4、5 | C. | 3、4 | D. | 4、3 |
3.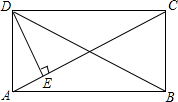 已知:如图,在矩形ABCD中,DE⊥AC,∠ADE=$\frac{1}{3}$∠CDE,那么∠BDC等于( )
已知:如图,在矩形ABCD中,DE⊥AC,∠ADE=$\frac{1}{3}$∠CDE,那么∠BDC等于( )
 已知:如图,在矩形ABCD中,DE⊥AC,∠ADE=$\frac{1}{3}$∠CDE,那么∠BDC等于( )
已知:如图,在矩形ABCD中,DE⊥AC,∠ADE=$\frac{1}{3}$∠CDE,那么∠BDC等于( )| A. | 60° | B. | 45° | C. | 30° | D. | 22.5° |
20. 如图,直线m∥n,∠1=70°,∠2=30°,则∠A等于( )
如图,直线m∥n,∠1=70°,∠2=30°,则∠A等于( )
 如图,直线m∥n,∠1=70°,∠2=30°,则∠A等于( )
如图,直线m∥n,∠1=70°,∠2=30°,则∠A等于( )| A. | 30° | B. | 35° | C. | 40° | D. | 50° |
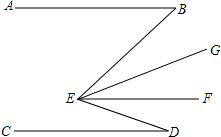 如图,AB∥EF∥CD,EG平分∠BEF,∠B+∠BED+∠D=192°,∠B-∠D=24°,则∠GEF=30°.
如图,AB∥EF∥CD,EG平分∠BEF,∠B+∠BED+∠D=192°,∠B-∠D=24°,则∠GEF=30°. 如图,菱形ABCD的对角线长分别为a、b.它的面积为S,以菱形ABCD各边中点为顶点作四边形A1B1C1D1,它的面积为S1,然后再以四边形A1B1C1D1的中点为顶点作四边形如此下去,得到四边形A2B2C2D2,它的面积为S2,如此下去,得到四边形AnBnCnDn,
如图,菱形ABCD的对角线长分别为a、b.它的面积为S,以菱形ABCD各边中点为顶点作四边形A1B1C1D1,它的面积为S1,然后再以四边形A1B1C1D1的中点为顶点作四边形如此下去,得到四边形A2B2C2D2,它的面积为S2,如此下去,得到四边形AnBnCnDn,