题目内容
10. 如图,矩形OABC的顶点A、C的坐标分别为(0,10)、(4,0),反比例函数y=$\frac{k}{x}(k≠0)$在第一象限内的图象过矩形OABC的对角线的交点M,并与AB、BC分别交于点E、F,连接OE、EF、OF,则△OEF的面积为$\frac{75}{4}$.
如图,矩形OABC的顶点A、C的坐标分别为(0,10)、(4,0),反比例函数y=$\frac{k}{x}(k≠0)$在第一象限内的图象过矩形OABC的对角线的交点M,并与AB、BC分别交于点E、F,连接OE、EF、OF,则△OEF的面积为$\frac{75}{4}$.
分析 先由矩形的性质得出B(4,10),M(2,5),利用待定系数法求出反比例函数的解析式为y=$\frac{10}{x}$,再求出E(1,10),F(4,$\frac{5}{2}$),然后根据△OEF的面积=S矩形OABC-S△OAE-S△BEF,代入数值计算即可.
解答  解:∵矩形OABC的顶点A、C的坐标分别为(0,10)、(4,0),
解:∵矩形OABC的顶点A、C的坐标分别为(0,10)、(4,0),
∴B(4,10),
∵M是矩形OABC对角线的交点,
∴OM=MB,
∴M点的坐标是(2,5),
把x=2,y=5代入y=$\frac{k}{x}(k≠0)$,得k=10,
∴反比例函数的解析式为y=$\frac{10}{x}$,
当y=10时,x=1,∴E(1,10);
当x=4时,y=$\frac{5}{2}$,∴F(4,$\frac{5}{2}$).
△OEF的面积=S矩形OABC-S△OAE-S△BEF
=10×4-$\frac{1}{2}$×10×1-$\frac{1}{2}$×4×$\frac{5}{2}$-$\frac{1}{2}$×3×$\frac{15}{2}$
=40-5-5-$\frac{45}{4}$
=$\frac{75}{4}$.
故答案为$\frac{75}{4}$.
点评 本题考查了矩形的性质,待定系数法求反比例函数的解析式,反比例函数图象上点的坐标特征,三角形的面积,求出点E、F的坐标是解题的关键.

练习册系列答案
相关题目
1.下列汽车标志中,可以看作中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
18.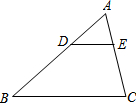 如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,若DE=2,BC=5,则AD:DB=( )
如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,若DE=2,BC=5,则AD:DB=( )
 如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,若DE=2,BC=5,则AD:DB=( )
如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,若DE=2,BC=5,则AD:DB=( )| A. | 3:2 | B. | 3:5 | C. | 2:5 | D. | 2:3 |
19.已知O是矩形ABCD的对角线的交点,AB=6,BC=8,则点O到AB、BC的距离分别是( )
| A. | 3、5 | B. | 4、5 | C. | 3、4 | D. | 4、3 |
20. 如图,直线m∥n,∠1=70°,∠2=30°,则∠A等于( )
如图,直线m∥n,∠1=70°,∠2=30°,则∠A等于( )
 如图,直线m∥n,∠1=70°,∠2=30°,则∠A等于( )
如图,直线m∥n,∠1=70°,∠2=30°,则∠A等于( )| A. | 30° | B. | 35° | C. | 40° | D. | 50° |
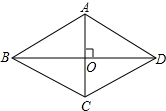 如图,四边形ABCD是菱形,对角线AC与BD相交于点O,AC=24,BD=10,求菱形ABCD的周长.
如图,四边形ABCD是菱形,对角线AC与BD相交于点O,AC=24,BD=10,求菱形ABCD的周长.