题目内容
4.已知y=y1-y2,且y1与x+1成反比例,y2与x2成正比例,当x=1时,y=-2;当x=-2时,y=-14.(1)求变量y与x之间的函数关系式;
(2)当x=-3时,求y的值.
分析 (1)根据已知条件设y1=$\frac{{k}_{1}}{x+1}$,y2=k2x2(k1≠0,k2≠0),得到y=$\frac{{k}_{1}}{x+1}$-k2x2,把当x=1时,y=-2;x=-2时,y=-14代入上式得方程组,解方程组即可得到结论;
(2)把x=-3代入y=$\frac{2}{x+1}$-3x2解方程即可得到结论
解答 解:(1)∵y1与x+1成反比例,y2与x2成正比例,
∴y1=$\frac{{k}_{1}}{x+1}$,y2=k2x2(k1≠0,k2≠0),
∵y=y1-y2,
∴y=$\frac{{k}_{1}}{x+1}$-k2x2,
∵当x=1时,y=-2;x=-2时,y=-14,
∴$\left\{\begin{array}{l}{\frac{{k}_{1}}{2}-{k}_{2}=-2}\\{-{k}_{1}-4{k}_{2}=-14}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{1}=2}\\{{k}_{2}=3}\end{array}\right.$,
∴函数解析式为:y=$\frac{2}{x+1}$-3x2,
(2)把x=-3代入y=$\frac{2}{x+1}$-3x2得:y=-28.
点评 此题主要考查了待定系数法求函数解析式,关键是掌握待定系数法求函数解析式的方法.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
19.已知O是矩形ABCD的对角线的交点,AB=6,BC=8,则点O到AB、BC的距离分别是( )
| A. | 3、5 | B. | 4、5 | C. | 3、4 | D. | 4、3 |
20. 如图,直线m∥n,∠1=70°,∠2=30°,则∠A等于( )
如图,直线m∥n,∠1=70°,∠2=30°,则∠A等于( )
 如图,直线m∥n,∠1=70°,∠2=30°,则∠A等于( )
如图,直线m∥n,∠1=70°,∠2=30°,则∠A等于( )| A. | 30° | B. | 35° | C. | 40° | D. | 50° |
14.下列等式中,是一元一次方程的是( )
| A. | x2-3x+2=0 | B. | 3+1=4 | C. | 2x=0 | D. | x+y=1 |
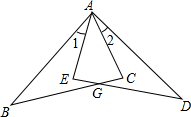 如图,在Rt△ACB和Rt△AED中,己知AB=AD,∠1=∠2,求证:EG=CG.
如图,在Rt△ACB和Rt△AED中,己知AB=AD,∠1=∠2,求证:EG=CG.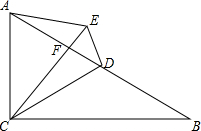 如图,在△ABC中,∠ACB=90°,∠B=30°,且点D是AB的中点,E为△ABC外一点,连接AE、DE,连接CE交AB于F,且∠CAD=∠CED.
如图,在△ABC中,∠ACB=90°,∠B=30°,且点D是AB的中点,E为△ABC外一点,连接AE、DE,连接CE交AB于F,且∠CAD=∠CED. 如图,菱形ABCD的对角线长分别为a、b.它的面积为S,以菱形ABCD各边中点为顶点作四边形A1B1C1D1,它的面积为S1,然后再以四边形A1B1C1D1的中点为顶点作四边形如此下去,得到四边形A2B2C2D2,它的面积为S2,如此下去,得到四边形AnBnCnDn,
如图,菱形ABCD的对角线长分别为a、b.它的面积为S,以菱形ABCD各边中点为顶点作四边形A1B1C1D1,它的面积为S1,然后再以四边形A1B1C1D1的中点为顶点作四边形如此下去,得到四边形A2B2C2D2,它的面积为S2,如此下去,得到四边形AnBnCnDn,