题目内容
17.在4(x-1)(x+2)=5,x2+y2=1,5x2-10=0,2x2+8x=0,$\frac{1}{x}$=x2+3中,是一元二次方程的个数为( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 根据一元二次方程的定义:只含有一个未知数,并且未知数的最高次数是2的整式方程叫一元二次方程进行分析即可.
解答 解:4(x-1)(x+2)=5,5x2-10=0,2x2+8x=0,是一元二次方程,共3个,
故选:B.
点评 此题主要考查了一元二次方程的定义,关键是掌握一元二次方程必须同时满足三个条件:①整式方程,即等号两边都是整式;方程中如果有分母,那么分母中无未知数; ②只含有一个未知数; ③未知数的最高次数是2.

练习册系列答案
相关题目
8.计算$\frac{1}{3}$-$\frac{1}{2}$的结果是( )
| A. | -$\frac{1}{6}$ | B. | $\frac{1}{6}$ | C. | -$\frac{5}{6}$ | D. | $\frac{5}{6}$ |
5.下列几种组合中,恰不能密铺的是( )
| A. | 同样大小的任意四边形 | |
| B. | 边长相同的正三角形、正方形、正十二边形 | |
| C. | 边长相同的正十边形和正五角形 | |
| D. | 边长相同的正八边形和正三角形 |
18.下列计算正确的是( )
| A. | 3a-a=3 | B. | a2+a2=a4 | C. | (3a)-(2a)=6a | D. | (a2)3=a6 |
 如图,在直角坐标系中,过点P(x,0)作x轴的垂线分别交抛物线y=x2+2与直线y=-$\frac{1}{2}$x于A,B两点,以线段AB为对角线作正方形ADBC,已知点Q(a,b)为该抛物线上的点.
如图,在直角坐标系中,过点P(x,0)作x轴的垂线分别交抛物线y=x2+2与直线y=-$\frac{1}{2}$x于A,B两点,以线段AB为对角线作正方形ADBC,已知点Q(a,b)为该抛物线上的点.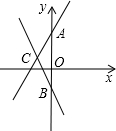 如图,已知直线y=2x+4与直线y=-2x-2相交于点C.
如图,已知直线y=2x+4与直线y=-2x-2相交于点C.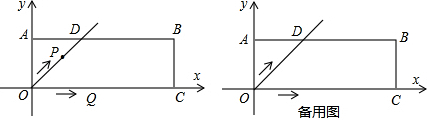
 已知:如图,在矩形ABCD中,AB=3,点E在AB的延长线上,且AE=AC,联结CE,取CE的中点F,联结BF、DF.
已知:如图,在矩形ABCD中,AB=3,点E在AB的延长线上,且AE=AC,联结CE,取CE的中点F,联结BF、DF.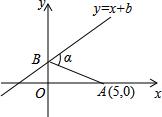 如图,已知A点坐标为(5,0),直线y=x+b与y轴交于点B,连接AB,α=75°,则b的值为$\frac{5\sqrt{3}}{3}$.
如图,已知A点坐标为(5,0),直线y=x+b与y轴交于点B,连接AB,α=75°,则b的值为$\frac{5\sqrt{3}}{3}$.