题目内容
7. 如图,在直角坐标系中,过点P(x,0)作x轴的垂线分别交抛物线y=x2+2与直线y=-$\frac{1}{2}$x于A,B两点,以线段AB为对角线作正方形ADBC,已知点Q(a,b)为该抛物线上的点.
如图,在直角坐标系中,过点P(x,0)作x轴的垂线分别交抛物线y=x2+2与直线y=-$\frac{1}{2}$x于A,B两点,以线段AB为对角线作正方形ADBC,已知点Q(a,b)为该抛物线上的点.(1)写出AB的长度关于x的函数关系式,并指出AB的最小值;
(2)若x=1,当点Q在正方形ADBC边上(点A除外)时,求a的值.
(3)若a=-1时,当点Q在正方形ADBC的内部(包括边界)时,求x的取值范围.
分析 (1)由AB⊥x轴,表示出点A,B的坐标,进而求出AB的函数关系式,最后确定出它的最小值;
(2)先求得A、B的坐标,进而求得AB的长,根据正方形的性质,求得C、D的坐标,然后根据待定系数法求得直线AC的解析式,与抛物线联立方程,解方程即可求得Q的坐标,从而求得a;
(3)分两种情况:①当P在y轴的右侧时,根据题意列出x+1=x2+2-3,x+1=-$\frac{1}{2}$x+3;
②当P在y轴的左侧时,则-x-1=x2+2-3,-x-1=-$\frac{1}{2}$x+3;解方程即可求得.
解答 解:(1)∵过点P(x,0)作x轴的垂线分别交抛物线y=x2+2与直线y=-$\frac{1}{2}$x于A,B两点,
∴A(x,x2+2),B(x,-$\frac{1}{2}$x),
∴AB=x2+2-(-$\frac{1}{2}$x)=x2+2+$\frac{1}{2}$x=(x+$\frac{1}{4}$)2+$\frac{31}{16}$,
∴当x=-$\frac{1}{4}$时,AB的最小值为$\frac{31}{16}$.
(2)若x=1,则P(1,0),
∵过点P(1,0)作x轴的垂线分别交抛物线y=x2+2与直线y=-$\frac{1}{2}$x于A,B两点,
∴A(1,3),B(1,-$\frac{1}{2}$),
∴AB=$\frac{7}{2}$,
∴AB的一半为$\frac{7}{4}$,
∵以线段AB为对角线作正方形ADBC,
∴C,D的纵坐标为3-$\frac{7}{4}$=$\frac{5}{4}$,
∵点C的横坐标为1-$\frac{7}{4}$=-$\frac{3}{4}$,
∴C(-$\frac{3}{4}$,$\frac{5}{4}$),
∵A(1,3),
∴直线AC的解析式为y=x+2,
∴与抛物线y=x2+2联立得$\left\{\begin{array}{l}{y=x+2}\\{y={x}^{2}+2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=0}\\{y=2}\end{array}\right.$或$\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$(舍去),
∴Q(0,2),
∵点Q(a,b)为该抛物线上的点.
∴a=0.
(3)若a=-1,则Q的坐标为(-1,3),
①当P在y轴的右侧时,
∴x+1=x2+2-3,解得x1=2,x2=0(舍去),
-x+2=-$\frac{1}{2}$x,解得x=4,
∴2≤x≤4;
②当P在y轴的左侧时,
则-x-1=x2+2-3,解得x=-1,
-x-1=-$\frac{1}{2}$x+3,解得x=-$\frac{8}{3}$,
∴-$\frac{8}{3}$≤x≤-1;
综上,x的取值范围是2≤x≤4或-$\frac{8}{3}$≤x≤-1.
点评 本题是二次函数的综合题,考查了正方形的性质,求一次函数的解析式的方法,二次函数的解析式及极值的确定方法,根据题意列出方程是本题的关键.

 如图,在平行四边形ABCD中,AB=9cm,AD=11cm,AC,BD相交于点O,OE⊥BD,交AD于点E,则△ABE的周长为( )
如图,在平行四边形ABCD中,AB=9cm,AD=11cm,AC,BD相交于点O,OE⊥BD,交AD于点E,则△ABE的周长为( )| A. | 20cm | B. | 18cm | C. | 16cm | D. | 10cm |
 如图所示,直线a∥b,直线c与a、b相交,∠1=60°,则∠2等于( )
如图所示,直线a∥b,直线c与a、b相交,∠1=60°,则∠2等于( )| A. | 60° | B. | 30° | C. | 120° | D. | 50° |
| A. | 5、3、9 | B. | 5、3、8 | C. | 5、2、7 | D. | 5、3、6 |
| A. | y2-3y-4=y(y-3)-4 | B. | 1-4x+4x2=(1-2x)2 | C. | x2+y2=(x+y)(x-y) | D. | x-1=x(1-$\frac{1}{x}$) |
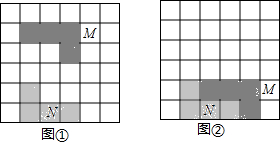 如图,在6×6方格中有两个涂有阴影的图形M、N,①中的图形M平移后位置如②所示,以下对图形M的平移方法叙述正确的是( )
如图,在6×6方格中有两个涂有阴影的图形M、N,①中的图形M平移后位置如②所示,以下对图形M的平移方法叙述正确的是( )| A. | 向右平移2个单位,向下平移3个单位 | |
| B. | 向右平移1个单位,向下平移3个单位 | |
| C. | 向右平移1个单位,向下平移4个单位 | |
| D. | 向右平移2个单位,向下平移4个单位 |
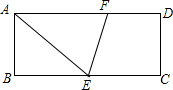 如图,在矩形ABCD中,E为BC边的中点,∠AEC的平分线交AD边于点F,若AB=3,AD=8,则FD的长为( )
如图,在矩形ABCD中,E为BC边的中点,∠AEC的平分线交AD边于点F,若AB=3,AD=8,则FD的长为( )