��Ŀ����
2����ƽ��ֱ������ϵxOy�У���ԭ��O����A��0��2����C��6��0��������OABC����AOC��ƽ���߽�AB�ڵ�D����P�ӵ�O��������ÿ��$\sqrt{2}$����λ���ȵ��ٶ�������OD�����ƶ���ͬʱ��Q�ӵ�O��������ÿ��2����λ���ȵ��ٶ���x���������ƶ������ƶ�ʱ��Ϊt�룮��1������P�ƶ�����Dʱ��t=2�룻
��2�����ӵ�A��C����ֱ��AC�Ľ���ʽ��
��3������M��ֱ��AC�ϵ�һ������һ�㣬�Ƿ����ijһʱ�̣�ʹ���ı���OPMQΪƽ���ı��Σ������ڣ���ֱ��д��t��ֵ����M�����ꣻ�������ڣ���˵�����ɣ�
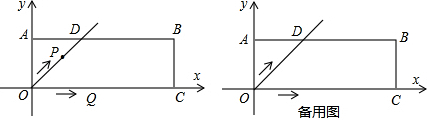
���� ��1�����ݾ����Լ���ƽ���ߵ����ʿɵó���OADΪ����ֱ�������Σ��ٸ��ݵ�A�������ϵ���ֱ�������ε����ʼ��ɵó�OD�ij��ȣ��Ӷ��ɵó�tֵ��
��2����ֱ��AC����ʽΪy=kx+b�����ݵ�A��C���������ڴ���ϵ�����������ֱ��AC�Ľ���ʽ��
��3��������ڣ��ҳ���P��O��Q��������꣬����ƽ���ı��ε�����--�Խ�����ƽ�֣��ֱ���OP��OQ��PQΪ�Խ��������M�����꣬�ٸ��ݵ�M��ֱ��AC�ϵ�һ������һ�㣬�������tֵ�Լ���M�����꣮
��� �⣺��1�����ı���OABCΪ���Σ��ҡ�AOC��ƽ���߽�AB�ڵ�D��
���OADΪ����ֱ�������Σ�
�ߵ�A��0��2����
��OA=2��OD=2$\sqrt{2}$��
��P�ƶ�����Dʱ��t=2$\sqrt{2}$��$\sqrt{2}$=2���룩��
�ʴ�Ϊ��2��
��2����ֱ��AC����ʽΪy=kx+b��
����A��0��2����C��6��0������y=kx+b��
�ã�$\left\{\begin{array}{l}{b=2}\\{6k+b=0}\end{array}\right.$����ã�$\left\{\begin{array}{l}{k=-\frac{1}{3}}\\{b=2}\end{array}\right.$��
��ֱ��AC����ʽΪy=-$\frac{1}{3}$x+2��
��3��������ڣ�����P��PE��x���ڵ�E����ͼ��ʾ��
�ɣ�1����֪��POEΪ����ֱ�������Σ�
���P��t��t����
O��0��0����Q��2t��0����
�ı���OPMQΪƽ���ı��η����������
����OPΪ�Խ���ʱ����M��0+t-2t��0+t-0��������-t��t����
�ߵ�M�ڵ�һ���ޣ�
������������Ҫ��
����OQΪ�Խ���ʱ����M��0+2t-t��0+0-t��������t��-t����
�ߵ�M�ڵ�һ���ޣ�
������������Ҫ��
����PQΪ�Խ���ʱ����M��t+2t-0��t+0-0��������3t��t����
�ߵ�M�ڵ�һ�����ڣ��ҵ�M��ֱ��AC�ϣ�
��t=-$\frac{1}{3}$��3t+2����ã�t=1��
��ʱ��M������Ϊ��3��1����
���Ͽ�֪������M��ֱ��AC�ϵ�һ������һ�㣬����ijһʱ�̣�ʹ���ı���OPMQΪƽ���ı��Σ���ʱt=1����M������Ϊ��3��1����
���� ���⿼���˾��ε����ʡ�����ֱ�������ε����ʡ�����ϵ������������ʽ�Լ�ƽ���ı��ε����ʣ�����Ĺؼ��ǣ���1������߶�OD�ij�����2�����ô���ϵ���������������ʽ����3��������������ۣ����������е��⣬�ѶȲ������������Ŀʱ������ƽ���ı��ε�����--�Խ�����ƽ�֣���ƽ���ı��ε�������������������ĸ�����������ǹؼ���

 ��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�| A�� | 5��3��9 | B�� | 5��3��8 | C�� | 5��2��7 | D�� | 5��3��6 |
| A�� | 4 | B�� | $\frac{1}{4}$ | C�� | -$\frac{1}{4}$ | D�� | -4 |
| A�� | 2�� | B�� | 3�� | C�� | 4�� | D�� | 5�� |
| A�� | x��0 | B�� | x��-3 | C�� | x��-3 | D�� | x��-3 |
| A�� | x2 | B�� | ��x+6��2 | C�� | ��x+2����x-6�� | D�� | ��x+2��2 |
| A�� | ��$\sqrt{4}$��2=4 | B�� | $\sqrt{��-4��^{2}}$=-4 | C�� | $\sqrt{��-4������-9��}$=$\sqrt{-4}$��$\sqrt{-9}$ | D�� | $\sqrt{7}$-$\sqrt{5}$=$\sqrt{2}$ |
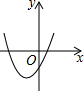
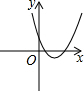
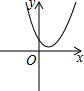
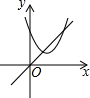 ��֪����������y=x����κ���y=ax2+bx+c��ͼ����ͼ��ʾ������κ���y=ax2+��b-1��x+c��ͼ������ǣ�������
��֪����������y=x����κ���y=ax2+bx+c��ͼ����ͼ��ʾ������κ���y=ax2+��b-1��x+c��ͼ������ǣ�������