题目内容
17.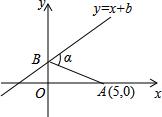 如图,已知A点坐标为(5,0),直线y=x+b与y轴交于点B,连接AB,α=75°,则b的值为$\frac{5\sqrt{3}}{3}$.
如图,已知A点坐标为(5,0),直线y=x+b与y轴交于点B,连接AB,α=75°,则b的值为$\frac{5\sqrt{3}}{3}$.
分析 令直线y=x+b与x轴交于点C,根据直线的解析式可求出点B、C的坐标,进而得出∠BCO=45°,再通过角的计算得出∠BAO=30°,根据点A的坐标利用特殊角的三角函数值即可得出b的值.
解答 解:令直线y=x+b与x轴交于点C,如图所示.
令y=x+b中x=0,则y=b,
∴B(0,b);
令y=x+b中y=0,则x=-b,
∴C(-b,0).
∴∠BCO=45°.
∵α=∠BCO+∠BAO=75°,
∴∠BAO=30°,
∵点A(5,0),
∴OA=5,OB=b=OA•tan∠BAO=$\frac{5\sqrt{3}}{3}$.
故答案为:$\frac{5\sqrt{3}}{3}$.
点评 本题考查了一次函数图象上点的坐标特征以及特殊角的三角函数值,解题的关键是求出∠BAO=30°.本题属于基础题,难度不大,解决该题型题目时,根据特殊角的三角函数值以及角的计算找出角的度数,再通过解直角三角形求出边的长度是关键.

练习册系列答案
相关题目
16.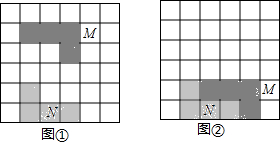 如图,在6×6方格中有两个涂有阴影的图形M、N,①中的图形M平移后位置如②所示,以下对图形M的平移方法叙述正确的是( )
如图,在6×6方格中有两个涂有阴影的图形M、N,①中的图形M平移后位置如②所示,以下对图形M的平移方法叙述正确的是( )
 如图,在6×6方格中有两个涂有阴影的图形M、N,①中的图形M平移后位置如②所示,以下对图形M的平移方法叙述正确的是( )
如图,在6×6方格中有两个涂有阴影的图形M、N,①中的图形M平移后位置如②所示,以下对图形M的平移方法叙述正确的是( )| A. | 向右平移2个单位,向下平移3个单位 | |
| B. | 向右平移1个单位,向下平移3个单位 | |
| C. | 向右平移1个单位,向下平移4个单位 | |
| D. | 向右平移2个单位,向下平移4个单位 |
5.设x是无理数,但(x-2)(x+6)是有理数,则下列式子中是有理数的是( )
| A. | x2 | B. | (x+6)2 | C. | (x+2)(x-6) | D. | (x+2)2 |
2.下列运算正确的是( )
| A. | ($\sqrt{4}$)2=4 | B. | $\sqrt{(-4)^{2}}$=-4 | C. | $\sqrt{(-4)×(-9)}$=$\sqrt{-4}$×$\sqrt{-9}$ | D. | $\sqrt{7}$-$\sqrt{5}$=$\sqrt{2}$ |
9.下列计算中,正确的是( )
| A. | a•a2=a2 | B. | 2a+3a=5a | C. | (2x3)2=6x3 | D. | (x2)3=x5 |
6.现有1角、5角硬币各10枚,从中取出16枚,共计4元,问1角、5角硬币各取多少枚?设1角、5角硬币各取x枚、y枚,可列方程( )
| A. | $\left\{\begin{array}{l}x+y=16\\ x+5y=4\end{array}\right.$ | B. | $\left\{\begin{array}{l}x+y=20\\ x+5y=4\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}x+y=20\\ 0.1x+0.5y=40\end{array}\right.$ | D. | $\left\{\begin{array}{l}x+y=16\\ x+5y=40\end{array}\right.$ |
 如图是江津区某一天的气温随时间变化的图象,根据图象回答:在这一天中:
如图是江津区某一天的气温随时间变化的图象,根据图象回答:在这一天中: