题目内容
12.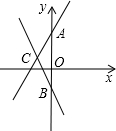 如图,已知直线y=2x+4与直线y=-2x-2相交于点C.
如图,已知直线y=2x+4与直线y=-2x-2相交于点C.(1)求两直线与y轴交点A、B的坐标;
(2)求△ABC的面积.
分析 (1)根据两直线解析式,分别令x=0求解即可得到点A、B的坐标;
(2)联立两直线解析式求出点C的坐标,再求出AB的长,然后根据三角形的面积公式列式计算即可得解.
解答 解:(1)对于直线y=2x+4,
令x=0,得到y=4,即A(0,4),
对于直线y=-2x-2,
令x=0,得到y=-2,即B(0,-2);
(2)联立得:$\left\{\begin{array}{l}{y=2x+4}\\{y=-2x-2}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{x=-\frac{3}{2}}\\{y=1}\end{array}\right.$,
即C(-$\frac{3}{2}$,1),
∵A(0,4),B(0,-2),
∴AB=6,
则S△ABC=$\frac{1}{2}$×6×$\frac{3}{2}$=$\frac{9}{2}$.
点评 本题考查了两直线相交的问题,直线与坐标轴的交点坐标的求解方法,联立两直线解析式求交点是常用的方法之一,要熟练掌握.

练习册系列答案
相关题目
20.下列方程中,是一元二次方程的是( )
| A. | 2x2-7=3y+1 | B. | $\frac{\sqrt{7}}{3}$x-$\sqrt{5}$=$\frac{{x}^{2}}{2}$+x | C. | 5x2-6y-2=0 | D. | ax2+bx+c=0 |
7.点A(x,y)在某反比例函数的图象上,xy=4,则此函数的表达式为( )
| A. | y=$\frac{4}{x}$ | B. | y=$\frac{8}{x}$ | C. | y=-$\frac{8}{x}$ | D. | y=-$\frac{4}{x}$ |
13.如果把分式$\frac{2x}{x-y}$中的x和y都扩大5倍,那么分式的值( )
| A. | 扩大5倍 | B. | 不变 | C. | 扩大10倍 | D. | 缩小$\frac{1}{5}$ |
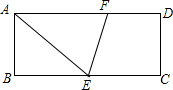 如图,在矩形ABCD中,E为BC边的中点,∠AEC的平分线交AD边于点F,若AB=3,AD=8,则FD的长为( )
如图,在矩形ABCD中,E为BC边的中点,∠AEC的平分线交AD边于点F,若AB=3,AD=8,则FD的长为( ) 如图是江津区某一天的气温随时间变化的图象,根据图象回答:在这一天中:
如图是江津区某一天的气温随时间变化的图象,根据图象回答:在这一天中: