题目内容
3.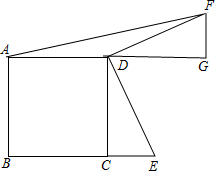 如图,在正方形ABCD中,AB=8,点E在BC的延长线上,将△CDE绕点D逆时针旋转90°至△GDF的位置,连结线段AF.如果△ADF的面积为12,那么线段BE的长为11.
如图,在正方形ABCD中,AB=8,点E在BC的延长线上,将△CDE绕点D逆时针旋转90°至△GDF的位置,连结线段AF.如果△ADF的面积为12,那么线段BE的长为11.
分析 由旋转的性质得:∠G=∠DCE=90°,FG=CE,由△ADF的面积为12可求得FG=3,继而可求得答案.
解答 解:由旋转的性质得:∠G=∠DCE=90°,FG=CE,
∵正方形ABCD中,AB=8,
∴AD=BC=8,
∵△ADF的面积为12,
∴$\frac{1}{2}$AD•FG=12,
∴FG=3,
∴BE=BC+CE=8+3=11,
故答案为:11.
点评 本题主要考查了旋转的性质,正方形的性质,三角形的面积公式,熟练掌握旋转的性质是解决问题的关键.

练习册系列答案
相关题目
11.已知2<x<3,化简:$\sqrt{({x-1)}^{2}}$+|x-3|的结果是( )
| A. | 2x-5 | B. | 5-2x | C. | -1 | D. | 2 |
18.圆锥的侧面展开图为半径为16,且圆心角为90°的扇形,则这个圆锥的底面半径为( )
| A. | 16 | B. | 4 | C. | 4$\sqrt{2}$ | D. | 8 |
8.已知⊙O的半径为r,其内接正六边形,正四边形,正三角形的边长分别为a,b,c,则a:b:c的值为( )
| A. | 1:2:3 | B. | 3:2:1 | C. | 1:$\sqrt{2}$:$\sqrt{3}$ | D. | $\sqrt{3}$:$\sqrt{2}$:1 |
12.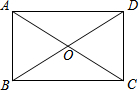 如图,四边形ABCD的对角线AC,BD相交于点O,且AC=BD,则下列条件能判定四边形ABCD为矩形的是( )
如图,四边形ABCD的对角线AC,BD相交于点O,且AC=BD,则下列条件能判定四边形ABCD为矩形的是( )
 如图,四边形ABCD的对角线AC,BD相交于点O,且AC=BD,则下列条件能判定四边形ABCD为矩形的是( )
如图,四边形ABCD的对角线AC,BD相交于点O,且AC=BD,则下列条件能判定四边形ABCD为矩形的是( )| A. | AB=CD | B. | OA=OC,OB=OD | C. | AC⊥BD | D. | AB∥CD,AD=BC |
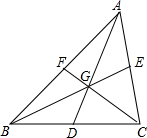 如图,△ABC的三条中线相交于点G.
如图,△ABC的三条中线相交于点G.