题目内容
15.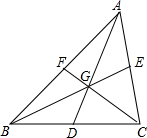 如图,△ABC的三条中线相交于点G.
如图,△ABC的三条中线相交于点G.(1)求证:$\overrightarrow{GD}$+$\overrightarrow{GE}$+$\overrightarrow{GF}$=$\overrightarrow{0}$;
(2)求证;$\overrightarrow{GA}$+$\overrightarrow{GB}$+$\overrightarrow{GC}$=$\overrightarrow{0}$.
分析 (1))由△ABC的三条中线相交于点G,可得$\overrightarrow{GD}$=$\frac{1}{3}$$\overrightarrow{AD}$,$\overrightarrow{GE}$=$\frac{1}{3}$$\overrightarrow{BE}$,$\overrightarrow{GF}$=$\frac{1}{3}$$\overrightarrow{CF}$,然后证得$\overrightarrow{AD}$+$\overrightarrow{BE}$+$\overrightarrow{CF}$=$\overrightarrow{0}$,即可证得结论;
(2)由△ABC的三条中线相交于点G,可得$\overrightarrow{GA}$=-$\frac{2}{3}$$\overrightarrow{AD}$,$\overrightarrow{GB}$=-$\frac{2}{3}$$\overrightarrow{BE}$,$\overrightarrow{GC}$=-$\frac{2}{3}$$\overrightarrow{CF}$,继而证得结论.
解答 证明:(1)∵△ABC的三条中线相交于点G,
∴$\overrightarrow{GD}$=$\frac{1}{3}$$\overrightarrow{AD}$,$\overrightarrow{GE}$=$\frac{1}{3}$$\overrightarrow{BE}$,$\overrightarrow{GF}$=$\frac{1}{3}$$\overrightarrow{CF}$,
∵$\overrightarrow{AD}$=$\overrightarrow{AB}$+$\overrightarrow{BD}$=$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{BC}$,$\overrightarrow{BE}$=$\overrightarrow{BA}$+$\overrightarrow{AE}$=$\overrightarrow{BA}$+$\frac{1}{2}$$\overrightarrow{AC}$,$\overrightarrow{CF}$=$\overrightarrow{CB}$+$\overrightarrow{BF}$=$\overrightarrow{CB}$+$\frac{1}{2}$$\overrightarrow{BA}$,
∴$\overrightarrow{AD}$+$\overrightarrow{BE}$+$\overrightarrow{CF}$=$\overrightarrow{CB}$+$\frac{1}{2}$($\overrightarrow{BC}$+$\overrightarrow{AC}$+$\overrightarrow{BA}$)=$\overrightarrow{CB}$+$\frac{1}{2}$($\overrightarrow{BC}$+$\overrightarrow{BC}$)=$\overrightarrow{CB}$+$\overrightarrow{BC}$=$\overrightarrow{0}$,
∴$\overrightarrow{GD}$+$\overrightarrow{GE}$+$\overrightarrow{GF}$=$\frac{1}{3}$($\overrightarrow{AD}$+$\overrightarrow{BE}$+$\overrightarrow{CF}$)=$\overrightarrow{0}$;
(2)∵△ABC的三条中线相交于点G,
∴$\overrightarrow{GA}$=-$\frac{2}{3}$$\overrightarrow{AD}$,$\overrightarrow{GB}$=-$\frac{2}{3}$$\overrightarrow{BE}$,$\overrightarrow{GC}$=-$\frac{2}{3}$$\overrightarrow{CF}$,
∴$\overrightarrow{GA}$+$\overrightarrow{GB}$+$\overrightarrow{GC}$=-$\frac{2}{3}$($\overrightarrow{AD}$+$\overrightarrow{BE}$+$\overrightarrow{CF}$)=$\overrightarrow{0}$.
点评 此题考查了平面向量的知识以及三角形重心的性质.注意掌握三角形法则的应用是解此题的关键.

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF;②∠DAF=15°;③AC垂直平分EF;④BE+DF=EF;⑤S△CEF=2S△ABE,其中正确结论有( )
如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF;②∠DAF=15°;③AC垂直平分EF;④BE+DF=EF;⑤S△CEF=2S△ABE,其中正确结论有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
| A. | -2 | B. | 3 | C. | 0 | D. | $\sqrt{6}$ |
| A. | $\sqrt{5}$ | B. | π | C. | 0 | D. | -6 |
 如图,AB∥CD,EC⊥CD于C,CF交AB于B,已知∠2=29°,则∠1的度数是( )
如图,AB∥CD,EC⊥CD于C,CF交AB于B,已知∠2=29°,则∠1的度数是( )| A. | 58° | B. | 59° | C. | 61° | D. | 62° |
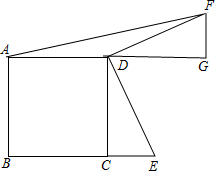 如图,在正方形ABCD中,AB=8,点E在BC的延长线上,将△CDE绕点D逆时针旋转90°至△GDF的位置,连结线段AF.如果△ADF的面积为12,那么线段BE的长为11.
如图,在正方形ABCD中,AB=8,点E在BC的延长线上,将△CDE绕点D逆时针旋转90°至△GDF的位置,连结线段AF.如果△ADF的面积为12,那么线段BE的长为11. 如图.双曲线y=$\frac{k}{x}$与直线y=x-2相交于A、B两点,点A的纵坐标为1.
如图.双曲线y=$\frac{k}{x}$与直线y=x-2相交于A、B两点,点A的纵坐标为1.