题目内容
8.已知⊙O的半径为r,其内接正六边形,正四边形,正三角形的边长分别为a,b,c,则a:b:c的值为( )| A. | 1:2:3 | B. | 3:2:1 | C. | 1:$\sqrt{2}$:$\sqrt{3}$ | D. | $\sqrt{3}$:$\sqrt{2}$:1 |
分析 根据题意画出图形,再由正多边形的性质及直角三角形的性质求解即可.
解答 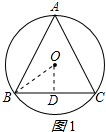 解:如图1所示,
解:如图1所示,
在正三角形ABC中,连接OB,过O作OD⊥BC于D,
则∠OBC=30°,BD=OB•cos30°=$\frac{\sqrt{3}}{2}$r,
故a=BC=2BD=$\sqrt{3}$r;
如图2所示,
在正方形ABCD中,连接OB、OC,过O作OE⊥BC于E,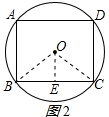 则△OBE是等腰直角三角形,
则△OBE是等腰直角三角形,
2BE2=OB2,即BE=$\frac{\sqrt{2}}{2}$r,
故b=BC=$\sqrt{2}$r;
如图3所示,
在正六边形ABCDEF中,连接OA、OB,过O作OG⊥AB,则△OAB是等边三角形,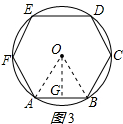 故AG=OA•cos60°=$\frac{1}{2}$r,
故AG=OA•cos60°=$\frac{1}{2}$r,
c=AB=2AG=r,
∴圆内接正三角形、正方形、正六边形的边长之比$\sqrt{3}$r:$\sqrt{2}$r:r=$\sqrt{3}$:$\sqrt{2}$:1.
故选:C.
点评 本题考查的是圆内接正三角形、正方形及正六边形的性质;根据题意画出图形,作出辅助线构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
13.下列命题中,假命题是( )
| A. | 邻角相等的平行四边形是矩形 | B. | 对角线垂直的平行四边形是矩形 | ||
| C. | 四个角相等的四边形是矩形 | D. | 对角线相等的平行四边形是矩形 |
17.估计$\sqrt{11}$的值在( )
| A. | 1和2之间 | B. | 2和3之间 | C. | 3和4之间 | D. | 4和5之间 |
 如图,EF∥AD,∠1=∠2,猜想∠BAC与∠DGA的关系,并说明理由.
如图,EF∥AD,∠1=∠2,猜想∠BAC与∠DGA的关系,并说明理由. 如图,正方形ACEF的边长为2,以AC为一边在同侧做等腰三角形ABC,且∠BAC=150°,BC交AE于点D,下列结论:①EF=ED;②S△DEC=1+$\frac{\sqrt{3}}{3}$;③AD+CD=BD,④S△ABD=$\frac{\sqrt{3}}{3}$,其中正确结论的序号是②③④.
如图,正方形ACEF的边长为2,以AC为一边在同侧做等腰三角形ABC,且∠BAC=150°,BC交AE于点D,下列结论:①EF=ED;②S△DEC=1+$\frac{\sqrt{3}}{3}$;③AD+CD=BD,④S△ABD=$\frac{\sqrt{3}}{3}$,其中正确结论的序号是②③④.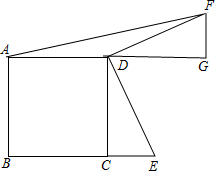 如图,在正方形ABCD中,AB=8,点E在BC的延长线上,将△CDE绕点D逆时针旋转90°至△GDF的位置,连结线段AF.如果△ADF的面积为12,那么线段BE的长为11.
如图,在正方形ABCD中,AB=8,点E在BC的延长线上,将△CDE绕点D逆时针旋转90°至△GDF的位置,连结线段AF.如果△ADF的面积为12,那么线段BE的长为11.