��Ŀ����
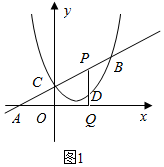
17����ͼ����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬ֱ��y=kx+3��x�ύ�ڵ�A����y�ύ�ڵ�C������C��������$y=\frac{1}{2}{x^2}+bx+c$��ֱ��AC������һ��B����B����Ϊ��$\frac{7}{2}$��$\frac{45}{8}$������1����ֱ�ߺ������ߵĽ���ʽ��
��2����P������CB�ϵ�һ�����㣬����P��ֱ��PQ��x�ᣬ����Ϊ��Q�����������ڵ�D��
�ٵ�PD=PCʱ�����P�����꣮
����x���ϵ�Q���Ҳ�ȡ��M��ʹMQ=$\frac{3}{2}$����QP���ӳ�����ȡ��N������PM��AN����֪tan��NAQ-tan��MPQ=$\frac{3}{4}$�����߶�PN�ij���

���� ��1��������y=kx+3ȷ��C�����꣬Ȼ���C���B���������y=$\frac{1}{2}$x2+bx+c�ù���b��c�ķ����飬Ȼ��ⷽ�������b��c���ɵõ������߽���ʽ��
��2�����Ȱ�B���������y=kx+3���k�õ�ֱ��AB�Ľ���ʽΪy=$\frac{3}{4}$x+3����ͼ1������һ�κ���ͼ��Ͷ��κ���ͼ���ϵ��������������P��t��$\frac{3}{4}$t+3������D��t��$\frac{1}{2}$t2-t+3��������t�ֱ��ʾ��PD��PC��������PD=PC�ɵõ�����t�ķ��̣�Ȼ��õ�����t������һԪ���η��̣��ٽⷽ���������������t��ֵ���Ӷ��õ�P�����ꣻ
����ͼ2��������ֱ��AB�Ľ���ʽȷ��A�����꣬��P��t��$\frac{3}{4}$t+3����Q��t��0���������t��ʾPQ��AQ�����������Ǻ����Ķ���ù���t�ķ��̣�Ȼ��ⷽ�̿����PN�ij���
���  �⣺��1����x=0ʱ��y=kx+3=3����C��0��3����
�⣺��1����x=0ʱ��y=kx+3=3����C��0��3����
��C��0��3����B��$\frac{7}{2}$��$\frac{45}{8}$������y=$\frac{1}{2}$x2+bx+c��$\left\{\begin{array}{l}{c=3}\\{\frac{1}{2}��\frac{49}{4}+\frac{7}{2}b+c=\frac{45}{8}}\end{array}\right.$�����$\left\{\begin{array}{l}{b=-1}\\{c=3}\end{array}\right.$
���������߽���ʽΪy=$\frac{1}{2}$x2-x+3��
��2���ٰ�B��$\frac{7}{2}$��$\frac{45}{8}$������y=kx+3��$\frac{7}{2}$k+3=$\frac{45}{8}$�����k=$\frac{3}{4}$��
����ֱ��AB�Ľ���ʽΪy=$\frac{3}{4}$x+3��
��ͼ1����P��t��$\frac{3}{4}$t+3������D��t��$\frac{1}{2}$t2-t+3����
����PD=|$\frac{1}{2}$t2-t+3-��$\frac{3}{4}$t+3��|=|$\frac{1}{2}$t2-$\frac{7}{4}$t|��
��PC=$\sqrt{{t}^{2}+��\frac{3}{4}t+3-3��^{2}}$=$\frac{5}{4}$t��
��ΪPD=PC��
����|$\frac{1}{2}$t2-$\frac{7}{4}$t|=$\frac{5}{4}$t��
��$\frac{1}{2}$t2-$\frac{7}{4}$t=$\frac{5}{4}$tʱ�����t1=0����ȥ����t2=6����ʱP������Ϊ��6��$\frac{15}{2}$����
��$\frac{1}{2}$t2-$\frac{7}{4}$t=-$\frac{5}{4}$tʱ�����t1=0����ȥ����t2=1����ʱP������Ϊ��1��$\frac{15}{4}$����
��������������������P������Ϊ��6��$\frac{15}{2}$����1��$\frac{15}{4}$����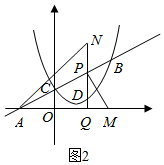 ����ͼ2����y=0ʱ��$\frac{3}{4}$x+3=0�����x=-4����A��-4��0����
����ͼ2����y=0ʱ��$\frac{3}{4}$x+3=0�����x=-4����A��-4��0����
��P��t��$\frac{3}{4}$t+3����Q��t��0������PQ=$\frac{3}{4}$t+3��AQ=t+4��
��Rt��NAQ��tan��NAQ=$\frac{NQ}{AQ}$=$\frac{NP+\frac{3}{4}t+3}{t+4}$��
��Rt��NMQ��tan��MPQ=$\frac{QM}{PQ}$=$\frac{\frac{3}{2}}{\frac{3}{4}t+3}$��
��tan��NAQ-tan��MPQ=$\frac{3}{4}$��
����$\frac{NP+\frac{3}{4}t+3}{t+4}$=$\frac{\frac{3}{2}}{\frac{3}{4}t+3}$��
����PN=2��
���� ���⿼���˶��κ������ۺ��⣺�������ն��κ���ͼ���ϵ���������������κ��������ʺ�������Ǻ����Ķ��壻�����ô���ϵ������������ʽ������������ͼ�����ʣ���ס�����ľ��빫ʽ�����һԪ���η��̣�

 �¿α�����Ķ�ѵ��ϵ�д�
�¿α�����Ķ�ѵ��ϵ�д� ������������Ӧ����ϵ�д�
������������Ӧ����ϵ�д�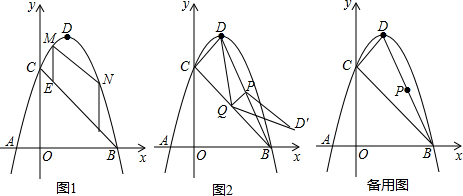
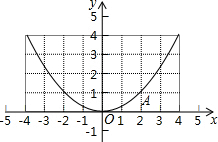 ��ͼ��һ�����κ�����ͼ������ԭ��O���ҹ���A��2��1����
��ͼ��һ�����κ�����ͼ������ԭ��O���ҹ���A��2��1����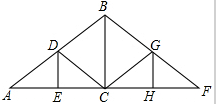 ��ͼ���ݼ����ͼ��һ���֣����С�A=30�㣬��D��б��AB���е㣬BC��DE��ֱ�ں���AC��AB=8m��������BC��DEҪ���
��ͼ���ݼ����ͼ��һ���֣����С�A=30�㣬��D��б��AB���е㣬BC��DE��ֱ�ں���AC��AB=8m��������BC��DEҪ���