题目内容
9.(1)解方程:$\frac{x}{x+2}$+$\frac{x+2}{2-x}$=$\frac{8}{x^2-4}$(2)求不等式组$\left\{\begin{array}{l}{\frac{1}{2}x+1<\frac{3}{2}}\\{1-5(x+1)≤6}\end{array}\right.$的解集.
分析 (1)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分即可确定出不等式组的解集.
解答 解:(1)去分母得:x2-2x-x2-4x-4=8,
解得:x=-2,
经检验x=-2是增根,分式方程无解;
(2)$\left\{\begin{array}{l}{\frac{1}{2}x+1<\frac{3}{2}①}\\{1-5(x+1)≤6②}\end{array}\right.$,
由①得:x<1,
由②得:x≥-2,
则不等式组的解集为-2≤x<1.
点评 此题考查了解分式方程,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
3.已知关于x的方程x2-2x+a=0有两个相等的实数根,则a的值为( )
| A. | -1 | B. | 0 | C. | 2 | D. | 1 |

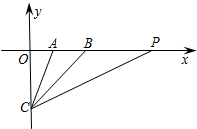 如图,在平面直角坐标系中,A(2,0),B(4,0),C(0,-4),CB平分∠ACP,则直线PC的解析式为y=$\frac{1}{2}$x-4.
如图,在平面直角坐标系中,A(2,0),B(4,0),C(0,-4),CB平分∠ACP,则直线PC的解析式为y=$\frac{1}{2}$x-4.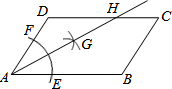 如图,在平行四边形ABCD中,AB>AD,按以下步骤作图:以A为圆心,小于AD的长为半径画弧,分别交AB、CD于E、F;再分别以E、F为圆心,大于$\frac{1}{2}$EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H,则下列结论正确的有:①③.
如图,在平行四边形ABCD中,AB>AD,按以下步骤作图:以A为圆心,小于AD的长为半径画弧,分别交AB、CD于E、F;再分别以E、F为圆心,大于$\frac{1}{2}$EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H,则下列结论正确的有:①③.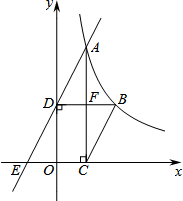 如图,已知函数y=$\frac{k}{x}$(x>0)的图象经过点A、B,点B的坐标为(2,2).过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,AC与BD交于点F.一次函数y=ax+b的图象经过点A、D,与x轴的负半轴交于点E.
如图,已知函数y=$\frac{k}{x}$(x>0)的图象经过点A、B,点B的坐标为(2,2).过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,AC与BD交于点F.一次函数y=ax+b的图象经过点A、D,与x轴的负半轴交于点E.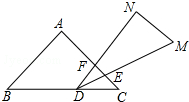 一副三角板叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角形的斜边上,AC与DM,DN分别交于点E、F,把△DEF绕点D旋转到一定位置,使得DE=DF,则∠BDN的度数是120°.
一副三角板叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角形的斜边上,AC与DM,DN分别交于点E、F,把△DEF绕点D旋转到一定位置,使得DE=DF,则∠BDN的度数是120°.