题目内容
5.解方程:$x+2\sqrt{x-3}=6$.分析 先移项,再两边平方,求出有理方程的解,最后检验即可.
解答 解:x+2$\sqrt{x-3}$=6,
2$\sqrt{x-3}$=6-x,
4(x-3)=(6-x)2,
4x-12=36-12x+x2,
x2-16x+48=0,
x1=4,x2=12,
当x1=4时,左边=4+2=6,左边=右边,
x1=4,是原方程的解,
当x2=12时,左边=12+6=18,左边≠右边,
x2=12不是原方程的解,
原方程的解是x=4.
点评 本题主要考查解无理方程,去掉根号把无理方程化成有理方程是解题的关键,注意观察方程的结构特点,把无理方程转化成一元二次方程的形式进行解答,需要同学们仔细掌握.

练习册系列答案
相关题目
20.一组数据1、2、3、4、5、15的平均数和中位数分别是( )
| A. | 5、5 | B. | 5、4 | C. | 5、3.5 | D. | 5、3 |
17.实数n、m是连续整数,如果$n<\sqrt{26}<m$,那么m+n的值是( )
| A. | 7 | B. | 9 | C. | 11 | D. | 13 |
 利用一面墙(墙的长度为24m),另三边用用58m长的篱笆围成一个面积为200m2的矩形场地,求矩形的长和宽.
利用一面墙(墙的长度为24m),另三边用用58m长的篱笆围成一个面积为200m2的矩形场地,求矩形的长和宽.

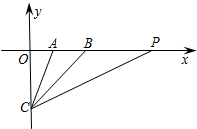 如图,在平面直角坐标系中,A(2,0),B(4,0),C(0,-4),CB平分∠ACP,则直线PC的解析式为y=$\frac{1}{2}$x-4.
如图,在平面直角坐标系中,A(2,0),B(4,0),C(0,-4),CB平分∠ACP,则直线PC的解析式为y=$\frac{1}{2}$x-4.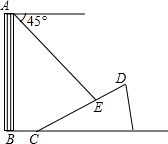 如图,一楼房AB后有一假山,其斜坡CD坡比为1:$\sqrt{3}$,山坡坡面上点E处有一休息亭,测得假山坡脚C与楼房水平距离BC=6米,与亭子距离CE=20米,小丽从楼房顶测得点E的俯角为45°.
如图,一楼房AB后有一假山,其斜坡CD坡比为1:$\sqrt{3}$,山坡坡面上点E处有一休息亭,测得假山坡脚C与楼房水平距离BC=6米,与亭子距离CE=20米,小丽从楼房顶测得点E的俯角为45°.