题目内容
6.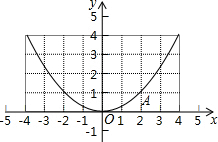 如图是一个二次函数的图象,顶点是原点O,且过点A(2,1),
如图是一个二次函数的图象,顶点是原点O,且过点A(2,1),(1)求出二次函数的表达式;
(2)我们把横、纵坐标都为整数的点称为整点,请用整数n表示这条抛物线上所有的整点坐标.
(3)过y轴的正半轴上一点C(0,a)作AO的平行线交抛物线于点B,
①求出直线BC的函数表达式(用a表示);
②如果点B是整点,求证:△OAB的面积是偶数.
分析 (1)可设抛物线的解析式为y=ax2,然后只需把点A的坐标代入抛物线的解析式,就可解决问题;
(2)由抛物线的解析式可知,要使y是整数,只需x是偶数,故x可用2n表示(n为整数),由此就可解决问题;
(3)①可运用待定系数法求出直线OA的解析式,然后根据两直线平行一次项的系数相同,就可得到直线BC的函数表达式;②由于点B是整点,点B的坐标可表示为(2n,n2),代入直线BC的解析式,即可得到a的值(用n表示),然后根据平行等积法可得S△OAB=S△OAC=n(n-1),由于n与n-1是相邻整数,必然一奇一偶,因而n(n-1)是偶数,问题得以解决.
解答 解:(1)设抛物线的解析式为y=ax2,
把A(2,1)代入y=ax2,得
1=4a,
解得a=$\frac{1}{4}$,
∴二次函数的表达式为y=$\frac{1}{4}$x2;
(2)抛物线上整点坐标可表示为(2n,n2),其中n为整数;
(3)①设直线OA的解析式为y=kx,
把点A(2,1)代入y=kx,得
1=2k,
解得k=$\frac{1}{2}$,
∴直线OA的解析式为y=$\frac{1}{2}$x,
则过点C(0,a)与直线OA平行的直线的解析式为y=$\frac{1}{2}$x+a;
②证明:∵点B是整点,
∴点B的坐标可表示为(2n,n2),其中n为整数,
把B(2n,n2)代入y=$\frac{1}{2}$x+a,得
n2=n+a,
∴a=n2-n=n(n-1).
∵BC∥OA,
∴S△OAB=S△OAC=$\frac{1}{2}$×a×2=a=n(n-1).
∵n为整数,∴n与n-1一奇一偶,
∴n(n-1)是偶数,
∴△OAB的面积是偶数.
点评 本题主要考查了运用待定系数法求直线与抛物线的解析式、两直线平行问题、直线上点的坐标特征、平行等积法、奇数与偶数等知识,运用平行等积法是解决第(3)②小题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 5、5 | B. | 5、4 | C. | 5、3.5 | D. | 5、3 |

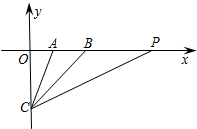 如图,在平面直角坐标系中,A(2,0),B(4,0),C(0,-4),CB平分∠ACP,则直线PC的解析式为y=$\frac{1}{2}$x-4.
如图,在平面直角坐标系中,A(2,0),B(4,0),C(0,-4),CB平分∠ACP,则直线PC的解析式为y=$\frac{1}{2}$x-4.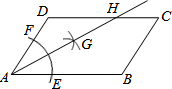 如图,在平行四边形ABCD中,AB>AD,按以下步骤作图:以A为圆心,小于AD的长为半径画弧,分别交AB、CD于E、F;再分别以E、F为圆心,大于$\frac{1}{2}$EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H,则下列结论正确的有:①③.
如图,在平行四边形ABCD中,AB>AD,按以下步骤作图:以A为圆心,小于AD的长为半径画弧,分别交AB、CD于E、F;再分别以E、F为圆心,大于$\frac{1}{2}$EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H,则下列结论正确的有:①③.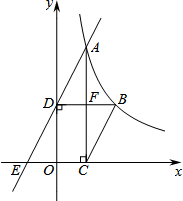 如图,已知函数y=$\frac{k}{x}$(x>0)的图象经过点A、B,点B的坐标为(2,2).过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,AC与BD交于点F.一次函数y=ax+b的图象经过点A、D,与x轴的负半轴交于点E.
如图,已知函数y=$\frac{k}{x}$(x>0)的图象经过点A、B,点B的坐标为(2,2).过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,AC与BD交于点F.一次函数y=ax+b的图象经过点A、D,与x轴的负半轴交于点E.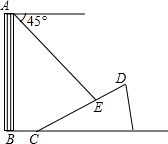 如图,一楼房AB后有一假山,其斜坡CD坡比为1:$\sqrt{3}$,山坡坡面上点E处有一休息亭,测得假山坡脚C与楼房水平距离BC=6米,与亭子距离CE=20米,小丽从楼房顶测得点E的俯角为45°.
如图,一楼房AB后有一假山,其斜坡CD坡比为1:$\sqrt{3}$,山坡坡面上点E处有一休息亭,测得假山坡脚C与楼房水平距离BC=6米,与亭子距离CE=20米,小丽从楼房顶测得点E的俯角为45°.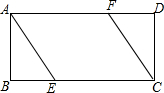 如图,E、F分别是矩形ABCD的边BC、AD上的点,且BE=DF
如图,E、F分别是矩形ABCD的边BC、AD上的点,且BE=DF