题目内容
2.如图,已知抛物线y=ax2+bx+3(a≠0)与x轴交于点A(-1,0),点B(3,0),与y轴交于点C,顶点为D,连接BC.(1)求抛物线的解析式及顶点D的坐标;
(2)如图1,点E,F为线段BC上的两个动点,且$EF=2\sqrt{2}$,过点E,F作y轴的平行线EM,FN,分别与抛物线交于点M,N,连接MN,设四边形EFNM面积为S,求S的最大值和此时点M的坐标;
(3)如图2,连接BD,点P为BD的中点,点Q是线段BC上的一个动点,连接DQ,PQ,将△DPQ沿PQ翻折得到△D′PQ,当△D′PQ与△BCD重叠部分的面积是△BDQ面积的$\frac{1}{4}$时,求线段CQ的长.
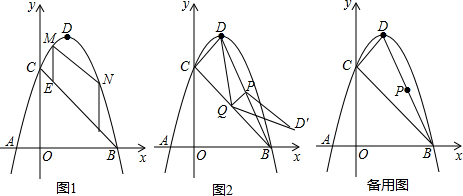
分析 (1)将点A和点B(3,0)坐标代入y=ax2+bx+3得到a和b的方程组,然后解方程求出a和b即可得到抛物线解析式,再把解析式配成顶点式即可得到D点坐标;
(2)先利用待定系数法求出直线BC的解析式,作FH⊥ME于H,如图1,利用△EHF为等腰直角三角形计算出FH,则可设E点的坐标为(m,-m+3),则F点的坐标为(m+2,-m+1),(0≤m≤1),接着表示出M点和N点坐标,则可计算出EM和FN,然后利用四边形EFNM面积为S=$\frac{1}{2}$×(EM+FN)×2得到面积与m的二次函数,再利用二次函数的性质解决问题;
(3)先利用勾股定理的逆定理证明△BCD为直角三角形,∠BCD=90°,再得到P(2,2),BP=$\frac{1}{2}$BD=$\sqrt{5}$,利用QP⊥DB,证明Rt△BPQ∽△BCD,通过相似比BQ,得到此时CQ的长,然后讨论:当CQ>$\frac{4\sqrt{2}}{3}$时,如图2,QD′交BD于G,利用△PQG的面积是△BDQ面积的$\frac{1}{4}$得到点G为PB的中点,则G($\frac{5}{2}$,1),PD=2PG,设Q(t,-t+3),利用两点间的距离公式用t表示DQ和QG,于是利用角平分线的性质定理得到得到关于t的方程,接着解方程求出t,从而得到此时CQ的长;当CQ<$\frac{4\sqrt{2}}{3}$时,如图3,PD′交BC于G,利用△PQG的面积是△BDQ面积的$\frac{1}{4}$得到点G为QB的中点,则可判断PG为△BDQ的中位线,再证明DQ=DP,设Q(t,-t+3),利用两点间的距离公式用t表示DQ,从而得到关于t的方程,接着解方程求出t,从而得到此时CQ的长.
解答 解:(1)将点A(-1,0),点B(3,0)代入抛物线解析式,得
$\left\{\begin{array}{l}{0=a-b+3}\\{0=9a+3b+3}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=-1}\\{b=2}\end{array}\right.$.
∴抛物线的解析式为y=-x2+2x+3.
∵抛物线的解析式为y=-x2+2x+3=-(x-1)2+4,
∴抛物线顶点D的坐标为(1,4).
(2)令x=0,则y=3,
∴点C的坐标为(0,3).
设直线BC的解析式为y=kx+3,
将点B(3,0)代入直线解析式,得0=3k+3,解得:k=-1,
∴直线BC的解析式为y=-x+3.
作FH⊥ME于H,如图1,∵OB=OC=3,
∴△OBC为等腰直角三角形,
∴△EHF为等腰直角三角形
∴FH=$\frac{\sqrt{2}}{2}$EF=$\frac{\sqrt{2}}{2}$×2$\sqrt{2}$=2,
设E点的坐标为(m,-m+3),则F点的坐标为(m+2,-m+1),(0≤m≤1);
∵ME∥y轴,NF∥y轴,
∴点M(m,-m2+2m+3),点N(m+2,-m2-2m+3),
∴EM=-m2+2m+3-(-m+3)=-m2+3m,FN=-m2-2m+3-(-m+1)=-m2-m+2.
四边形EFNM面积为S=$\frac{1}{2}$×(EM+FN)×2=-2(m2-m-1)=-2$(m-\frac{1}{2})^{2}$+$\frac{5}{2}$,
∴当m=$\frac{1}{2}$时,S取得最大值,最大值为$\frac{5}{2}$,此时点M的坐标为($\frac{1}{2}$,$\frac{15}{4}$).
(3)∵BC=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,CD=$\sqrt{{1}^{2}+(4-3)^{2}}$=$\sqrt{2}$,BD=$\sqrt{(3-1)^{2}+{4}^{2}}$=2$\sqrt{5}$,
而(3$\sqrt{2}$)2+($\sqrt{2}$)2=(2$\sqrt{5}$)2,
∴△BCD为直角三角形,∠BCD=90°,
∵点P为BD的中点,
∴P(2,2),BP=$\frac{1}{2}$BD=$\sqrt{5}$,
若QP⊥DB,∵∠PBQ=∠CBD,
∴Rt△BPQ∽△BCD,
∴BQ:BD=BP:BC,即BQ:2$\sqrt{5}$=$\sqrt{5}$:3$\sqrt{2}$,解得BQ=$\frac{5\sqrt{2}}{3}$,
此时CQ=3$\sqrt{2}$-$\frac{5\sqrt{2}}{3}$=$\frac{4\sqrt{2}}{3}$;
当CQ>$\frac{4\sqrt{2}}{3}$时,如图2,QD′交BD于G,
∵△PQG的面积是△BDQ面积的$\frac{1}{4}$,
而△PQB的面积为△BDQ面积的$\frac{1}{2}$,
∴△PQG的面积为△PBQ面积的$\frac{1}{2}$,
∴点G为PB的中点,
∴G($\frac{5}{2}$,1),PD=2PG,
设Q(t,-t+3),则DQ=$\sqrt{(t-1)^{2}+(-t+3-4)^{2}}$,QG=$\sqrt{(t-\frac{5}{2})^{2}+(-t+3-1)^{2}}$,
∵△DPQ沿PQ翻折得到△D′PQ,
∴∠DQP=∠GQP,即PQ平分∠DQG,
∴QD:QG=PD:PG=2:1,即QD=2QG,
∴$\sqrt{(t-1)^{2}+(-t+3-4)^{2}}$=2$\sqrt{(t-\frac{5}{2})^{2}+(-t+3-1)^{2}}$,
整理得2t2-12t=13=0,解得t1=$\frac{6+\sqrt{10}}{2}$(舍去),t2=$\frac{6-\sqrt{10}}{2}$,
此时CQ=$\sqrt{{t}^{2}+(-t+3-3)^{2}}$=$\sqrt{2}$t=$\sqrt{2}$×$\frac{6-\sqrt{10}}{2}$=3$\sqrt{2}$-$\sqrt{5}$;
当CQ<$\frac{4\sqrt{2}}{3}$时,如图3,PD′交BC于G,
∵△PQG的面积是△BDQ面积的$\frac{1}{4}$,
而△PQB的面积为△BDQ面积的$\frac{1}{2}$,
∴△PQG的面积为△PBQ面积的$\frac{1}{2}$,
∴点G为QB的中点,
∴PG为△BDQ的中位线,
∴DQ∥PG,
∴∠DQP=∠GPQ,
∵△DPQ沿PQ翻折得到△D′PQ,
∴∠DPQ=∠GPQ,
∴∠DQP=∠∠DPQ,
∴DQ=DP,
设Q(t,-t+3),DQ=$\sqrt{(t-1)^{2}+(-t+3-4)^{2}}$,
∴$\sqrt{(t-1)^{2}+(-t+3-4)^{2}}$=$\frac{1}{2}$×2$\sqrt{5}$,
整理得2t2-3=0,解得t1=-$\frac{\sqrt{6}}{2}$(舍去),t2=$\frac{\sqrt{6}}{2}$,
此时CQ=$\sqrt{{t}^{2}+(-t+3-3)^{2}}$=$\sqrt{2}$t=$\sqrt{2}$×$\frac{\sqrt{6}}{2}$=$\sqrt{3}$,
综上所述,CQ的长为$\sqrt{3}$或3$\sqrt{2}$-$\sqrt{5}$.
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和折叠的性质;会利用待定系数法求函数解析式;理解坐标与图形性质,记住两点间的距离公式;会解一元二次方程.

 综合自测系列答案
综合自测系列答案| A. | m≥3 | B. | m>3 | C. | m≤3 | D. | m<3 |
| A. | 7 | B. | 9 | C. | 11 | D. | 13 |

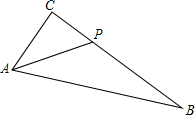 如图.在Rt△ABC中,∠C=90°,AC=6,BC=10.设P为BC上任一点,P点不与BC重合,且CP=x,若y表示△ABP的面积.
如图.在Rt△ABC中,∠C=90°,AC=6,BC=10.设P为BC上任一点,P点不与BC重合,且CP=x,若y表示△ABP的面积.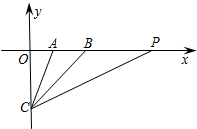 如图,在平面直角坐标系中,A(2,0),B(4,0),C(0,-4),CB平分∠ACP,则直线PC的解析式为y=$\frac{1}{2}$x-4.
如图,在平面直角坐标系中,A(2,0),B(4,0),C(0,-4),CB平分∠ACP,则直线PC的解析式为y=$\frac{1}{2}$x-4.