题目内容
12. 如图,四边形ACDE是证明勾股定理时用到的一个图形,a,b,c是Rt△ABC和Rt△BED边长,易知$AE=\sqrt{2}c$,这时我们把关于x的形如$a{x^2}+\sqrt{2}cx+b=0$的一元二次方程称为“勾系一元二次方程”.若x=-1是“勾系一元二次方程”$a{x^2}+\sqrt{2}cx+b=0$的一个根,且四边形ACDE的周长是$6\sqrt{2}$,求△ABC的面积.
如图,四边形ACDE是证明勾股定理时用到的一个图形,a,b,c是Rt△ABC和Rt△BED边长,易知$AE=\sqrt{2}c$,这时我们把关于x的形如$a{x^2}+\sqrt{2}cx+b=0$的一元二次方程称为“勾系一元二次方程”.若x=-1是“勾系一元二次方程”$a{x^2}+\sqrt{2}cx+b=0$的一个根,且四边形ACDE的周长是$6\sqrt{2}$,求△ABC的面积.
分析 利用根的意义和勾股定理作为相等关系先求得c的值,根据完全平方公式求得ab的值,从而可求得面积.
解答 解:当x=-1时,有a-$\sqrt{2}$c+b=0,即a+b=$\sqrt{2}$c
∵2a+2b+$\sqrt{2}$c=6$\sqrt{2}$,即2(a+b)+$\sqrt{2}$c=6$\sqrt{2}$,
∴3$\sqrt{2}$c=6$\sqrt{2}$,
∴c=2,
∴a2+b2=c2=4,a+b=2$\sqrt{2}$,
∵(a+b)2=a2+b2+2ab,
∴ab=2,
∴S△ABC=$\frac{1}{2}$ab=1.
点评 此类考查了勾股定理的证明,读懂题意,根据题目中所给的材料结合勾股定理和根的判别式解题是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,点B、C都在x轴上,AB⊥BC,垂足为B,M是AC的中点.若点A的坐标为(3,4),点M的坐标为(1,2),则点C的坐标为(-1,0).
如图,点B、C都在x轴上,AB⊥BC,垂足为B,M是AC的中点.若点A的坐标为(3,4),点M的坐标为(1,2),则点C的坐标为(-1,0).
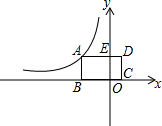 矩形ABCD在坐标系中如图所示放置.已知点B、C在x轴上,点A在第二象限,D(2,4),BC=6,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点A.
矩形ABCD在坐标系中如图所示放置.已知点B、C在x轴上,点A在第二象限,D(2,4),BC=6,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点A. 如图所示,二次函数y=ax2+bx+c的图象中,陈刚同学观察得出了下面四条结论:①b2-4ac>0;②c>1;③2a-b<0;④a+b+c<0.其中正确的序号有①③④.
如图所示,二次函数y=ax2+bx+c的图象中,陈刚同学观察得出了下面四条结论:①b2-4ac>0;②c>1;③2a-b<0;④a+b+c<0.其中正确的序号有①③④.