题目内容
4.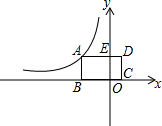 矩形ABCD在坐标系中如图所示放置.已知点B、C在x轴上,点A在第二象限,D(2,4),BC=6,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点A.
矩形ABCD在坐标系中如图所示放置.已知点B、C在x轴上,点A在第二象限,D(2,4),BC=6,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点A.(1)求k值;
(2)把矩形ABCD向左平移,使点C刚好与原点重合,此时线段AB与反比例函数y=$\frac{k}{x}$的交点坐标是什么?
分析 (1)根据矩形的性质求出点A的坐标,利用待定系数法求出k值;
(2)根据平移规律求出点B的坐标,计算即可.
解答 解:(1)∵点D的坐标为(2,4),BC=6,
∴OB=4,AB=4,
∴点A的坐标为(-4,4),
∵反比例函数y=$\frac{k}{x}$(x<0)的图象经过点A,
∴4=$\frac{k}{-4}$,
解得,k=-16;
(2)把矩形ABCD向左平移,使点C刚好与原点重合,
则点B的坐标为(-6,0),
当x=-6时,y=-$\frac{16}{-6}$=$\frac{8}{3}$,
∴此时线段AB与反比例函数y=$\frac{k}{x}$的交点坐标是(-6,$\frac{8}{3}$).
点评 本题考查的是反比例函数图象上点的坐标特征、矩形的性质、坐标与图形的变化,掌握矩形的性质、待定系数法求函数解析式的步骤是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15. 今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.下列说法错误的是( )
今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.下列说法错误的是( )
 今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.下列说法错误的是( )
今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.下列说法错误的是( )| A. | 小明中途休息用了20分钟 | |
| B. | 小明休息前爬山的平均速度为每分钟70米 | |
| C. | 小明休息后爬山的平均速度为每分钟38米 | |
| D. | 小明在上述过程中所走的路程为3800米 |
14.一次函数y=kx+b的图象与x轴、y轴的交点坐标分别是(-2,0),(0,-1),这个一次函数的解析式为( )
| A. | y=$\frac{1}{2}$x-1 | B. | y=2x+2 | C. | y=-x-1 | D. | y=2x-1 |
 如图,四边形ACDE是证明勾股定理时用到的一个图形,a,b,c是Rt△ABC和Rt△BED边长,易知$AE=\sqrt{2}c$,这时我们把关于x的形如$a{x^2}+\sqrt{2}cx+b=0$的一元二次方程称为“勾系一元二次方程”.若x=-1是“勾系一元二次方程”$a{x^2}+\sqrt{2}cx+b=0$的一个根,且四边形ACDE的周长是$6\sqrt{2}$,求△ABC的面积.
如图,四边形ACDE是证明勾股定理时用到的一个图形,a,b,c是Rt△ABC和Rt△BED边长,易知$AE=\sqrt{2}c$,这时我们把关于x的形如$a{x^2}+\sqrt{2}cx+b=0$的一元二次方程称为“勾系一元二次方程”.若x=-1是“勾系一元二次方程”$a{x^2}+\sqrt{2}cx+b=0$的一个根,且四边形ACDE的周长是$6\sqrt{2}$,求△ABC的面积. 如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°,得到△FEC
如图,在△ABC中,AB=AC,若将△ABC绕点C顺时针旋转180°,得到△FEC

