题目内容
11.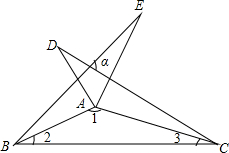 如图,把△ABC沿AB、AC翻折180°得到△ABE、△ACD,若∠1:∠2:∠3=28:5:3,则∠α的度数为80°.
如图,把△ABC沿AB、AC翻折180°得到△ABE、△ACD,若∠1:∠2:∠3=28:5:3,则∠α的度数为80°.
分析 根据三角形的内角和和折叠的性质计算即可.
解答 解:∵∠1:∠2:∠3=28:5:3,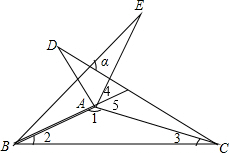
∴设∠1=28x,∠2=5x,∠3=3x,
由∠1+∠2+∠3=180°得:
28x+5x+3x=180°,
解得x=5,
故∠1=28×5=140°,∠2=5×5=25°,∠3=3×5=15°,
∵△ABE和△ADC是△ABC分别沿着AB、AC边翻折180°形成的,
∴∠DCA=∠E=∠3=15°,∠2=∠EBA=∠D=25°,∠4=∠EBA+∠E=25°+15°=40°,
∠5=∠2+∠3=25°+15°=40°,
故∠EAC=∠4+∠5=40°+40°=80°,
在△EGF与△CAF中,∠E=∠DCA,∠DFE=∠CFA,
∴△EGF∽△CAF,
∴α=∠EAC=80°.
故答案为:80°
点评 本题考查图形的折叠变化及三角形的内角和定理.关键是要理解折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,只是位置变化.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
19.两条平行线被第三条直线所截,则一对同位角的平分线的位置关系是( )
| A. | 互相垂直 | B. | 平行 | ||
| C. | 相交但不垂直 | D. | 平行或相交都有可能 |
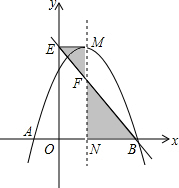 如图,抛物线y=-x2+2x+c与x轴交于A,B两点,它的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连接BE交MN于点F.
如图,抛物线y=-x2+2x+c与x轴交于A,B两点,它的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连接BE交MN于点F. 如图,平移△ABC可得到△DEF,若∠A=45°,∠C=65°,则∠E=70°,∠EDF=45°,∠DOB=65°.
如图,平移△ABC可得到△DEF,若∠A=45°,∠C=65°,则∠E=70°,∠EDF=45°,∠DOB=65°.