题目内容
6.设二次函数y=x2-2px-p的图象与x轴交于不同的两点A(x1,0),B(x2,0).(1)证明:2px1+x${\;}_{2}^{2}$+3p>0
(2)若|AB|<|2p-3|,求p的范围.
分析 (1)利用根与系数的关系以及方程的根的定义利用p表示出2px1+x${\;}_{2}^{2}$+3p,然后利用根的判别式即可证得;
(2)利用p表示出AB的长,则可以得到一个关于p的不等式,从而求解.
解答 解:(1)根据题意得:x1+x2=2p,x2x2=-p,x22-2px2-p=0,
则2px1+x22+3p
=2px1+2px2+p+3p
=2p(x1+x2)+4p
=4p2+4p,
∵△=(-2p)2+4p=4p2+4p>0,
∴2px1+x22+3p>0;
(2)AB=|x1-x2|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=2$\sqrt{{p}^{2}+p}$,
即2$\sqrt{{p}^{2}+p}$<|2p-3|,
即(2$\sqrt{{p}^{2}+p}$)2<(2p-3)2,
4p2+4p<4p2-12p+9,
∴p<$\frac{9}{16}$,
又∵4p2+4p>0,
p2+p>0,p(p+1)>0,
∴p<-1或p>0.
综上0<p<$\frac{9}{16}$.
点评 本题考查了二次函数与x轴的交点与对应的一元二次方程的关系,与x轴的交点的横坐标就是方程的解.

练习册系列答案
相关题目
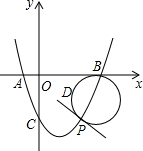 如图,抛物线y=x2-2x-3与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,点D的坐标为(1,-1),P是第四象限内抛物线上一动点,以PB为直径的圆经过点D,求经过点P且和这个圆相切的直线的解析式.
如图,抛物线y=x2-2x-3与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,点D的坐标为(1,-1),P是第四象限内抛物线上一动点,以PB为直径的圆经过点D,求经过点P且和这个圆相切的直线的解析式.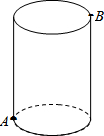 如图,圆柱的高为8cm,底面半径为2cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,它需要爬行的最短路程是多少厘米?(圆周率取3)
如图,圆柱的高为8cm,底面半径为2cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,它需要爬行的最短路程是多少厘米?(圆周率取3)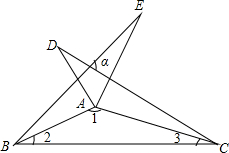 如图,把△ABC沿AB、AC翻折180°得到△ABE、△ACD,若∠1:∠2:∠3=28:5:3,则∠α的度数为80°.
如图,把△ABC沿AB、AC翻折180°得到△ABE、△ACD,若∠1:∠2:∠3=28:5:3,则∠α的度数为80°.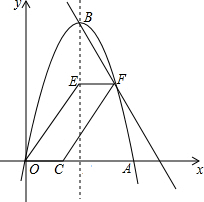 如图,抛物线y=-x2+6x与x轴交于点O,A,顶点为B,动点E在抛物线对称轴上,点F在对称轴右侧抛物线上,点C在x轴正半轴上,且EF$\stackrel{∥}{=}$OC,连接OE,CF得四边形OCFE.
如图,抛物线y=-x2+6x与x轴交于点O,A,顶点为B,动点E在抛物线对称轴上,点F在对称轴右侧抛物线上,点C在x轴正半轴上,且EF$\stackrel{∥}{=}$OC,连接OE,CF得四边形OCFE.