题目内容
2.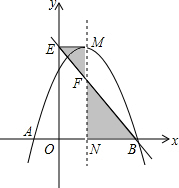 如图,抛物线y=-x2+2x+c与x轴交于A,B两点,它的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连接BE交MN于点F.
如图,抛物线y=-x2+2x+c与x轴交于A,B两点,它的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连接BE交MN于点F.(1)求顶点M的坐标(用含c的代数式表示);
(2)若△EMF与△BNF的面积相等,求该抛物线的解析式.
分析 (1)由抛物线的顶点坐标公式即可得出结果;
(2)由平行线的性质得出△MEF∽△NBF,由已知条件得出△EMF≌△BNF,得出BN=ME=1,因此B(2,0),代入抛物线解析式求出c=0,即可得出结果.
解答 解:(1)抛物线y=-x2+2x+c,
-$\frac{b}{2a}$=-$\frac{2}{-2}$=1,$\frac{4ac-{b}^{2}}{4a}$=$\frac{-4c-4}{-4}$=-c+1,
∴N(1,c+1);
(2)∵NE∥BN,
∴△MEF∽△NBF,
∵△EMF与△BNF的面积相等,
∴相似比为1,
∴△EMF≌△BNF,
∴BN=ME=1,
∴B(2,0),代入抛物线解析式得:0=-4+4+c,
解得:c=0,
∴y=-x2+2x.
点评 本题考查了抛物线与x轴的交点坐标、顶点坐标公式、相似三角形的判定、全等三角形的判定与性质、抛物线解析式的求法;由已知条件得出BN=ME=1是解决问题(2)的关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
4.下列四个数中,是无理数的是( )
| A. | $\frac{π}{2}$ | B. | $\frac{22}{7}$ | C. | $\root{3}{-8}$ | D. | ($\sqrt{3}$)2 |
12.下列图形中是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,在平面直角坐标系中,⊙D与y轴相切于点C(0,4),与x轴相交于A、B两点,且AB=6.
如图,在平面直角坐标系中,⊙D与y轴相切于点C(0,4),与x轴相交于A、B两点,且AB=6.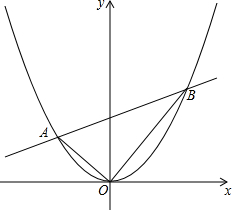 已知A,B是抛物线y=$\frac{1}{4}$x2上的两点,且OA⊥OB.(O为原点)
已知A,B是抛物线y=$\frac{1}{4}$x2上的两点,且OA⊥OB.(O为原点)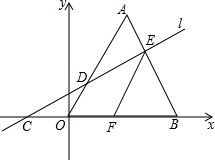 如图,在平面直角坐标系中,△A0B是边长为3的等边三角形,直线l与x轴、0A、AB分别交于点C、D、E,0C=AE.过点E作EF∥0A,交x轴于点F.
如图,在平面直角坐标系中,△A0B是边长为3的等边三角形,直线l与x轴、0A、AB分别交于点C、D、E,0C=AE.过点E作EF∥0A,交x轴于点F.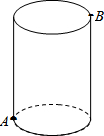 如图,圆柱的高为8cm,底面半径为2cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,它需要爬行的最短路程是多少厘米?(圆周率取3)
如图,圆柱的高为8cm,底面半径为2cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,它需要爬行的最短路程是多少厘米?(圆周率取3)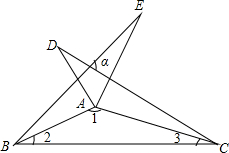 如图,把△ABC沿AB、AC翻折180°得到△ABE、△ACD,若∠1:∠2:∠3=28:5:3,则∠α的度数为80°.
如图,把△ABC沿AB、AC翻折180°得到△ABE、△ACD,若∠1:∠2:∠3=28:5:3,则∠α的度数为80°.