题目内容
19.两条平行线被第三条直线所截,则一对同位角的平分线的位置关系是( )| A. | 互相垂直 | B. | 平行 | ||
| C. | 相交但不垂直 | D. | 平行或相交都有可能 |
分析 利用平行线的性质:两直线平行,同位角相等.那么同位角的平分线所分得的角也相等,再根据同位角相等,两直线平行的判定就可证明.
解答 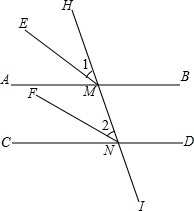 解:如图,AB∥CD,HI与AB,CD分别交于点M、N,EM,FN分别是∠AMH,∠CNH的平分线,
解:如图,AB∥CD,HI与AB,CD分别交于点M、N,EM,FN分别是∠AMH,∠CNH的平分线,
∵AB∥CD,
∴∠AMH=∠CNH(两直线平行,同位角相等),
∵EM,FN分别是∠AMH,∠CNH的平分线,
∴∠1=∠2,
∴EM∥FN(同位角相等,两直线平行),
∴∠1=$\frac{1}{2}$∠AMH,∠2=$\frac{1}{2}$∠CNH,
∴∠1=∠2,
∴EM∥FN(同位角相等,两直线平行).
故选:B.
点评 此题考查了平行线的判定与角平分线的定义.注意文字题的求解方法:首先根据题意画图,用数学语言表示出已知求证,再证明.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.比较(27)4与(34)3的大小,可得( )
| A. | (27)4=(34)3 | B. | (27)4>(34)3 | C. | (27)4<(34)3 | D. | 无法确定 |
9.下列多项式中,能直接用公式法分解因式的是( )
| A. | x2-xy2 | B. | x2+xy+y2 | C. | 4x2-4x-1 | D. | x2-4x+4 |
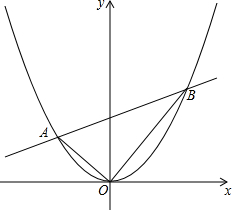 已知A,B是抛物线y=$\frac{1}{4}$x2上的两点,且OA⊥OB.(O为原点)
已知A,B是抛物线y=$\frac{1}{4}$x2上的两点,且OA⊥OB.(O为原点)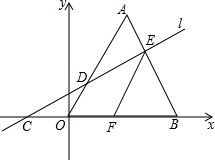 如图,在平面直角坐标系中,△A0B是边长为3的等边三角形,直线l与x轴、0A、AB分别交于点C、D、E,0C=AE.过点E作EF∥0A,交x轴于点F.
如图,在平面直角坐标系中,△A0B是边长为3的等边三角形,直线l与x轴、0A、AB分别交于点C、D、E,0C=AE.过点E作EF∥0A,交x轴于点F.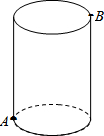 如图,圆柱的高为8cm,底面半径为2cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,它需要爬行的最短路程是多少厘米?(圆周率取3)
如图,圆柱的高为8cm,底面半径为2cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,它需要爬行的最短路程是多少厘米?(圆周率取3)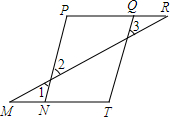 如图,M、N、T和A、B、C分别在同一直线上,且∠1=∠3,∠P=∠T,求证:PQ∥MT.
如图,M、N、T和A、B、C分别在同一直线上,且∠1=∠3,∠P=∠T,求证:PQ∥MT.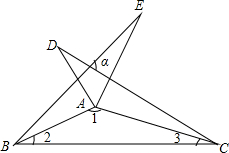 如图,把△ABC沿AB、AC翻折180°得到△ABE、△ACD,若∠1:∠2:∠3=28:5:3,则∠α的度数为80°.
如图,把△ABC沿AB、AC翻折180°得到△ABE、△ACD,若∠1:∠2:∠3=28:5:3,则∠α的度数为80°.