题目内容
20.已知一副直角三角板如图放置,其中BC=3,EF=4,把30°的三角板向右平移,使顶点B落在45°的三角板的斜边DF上,则两个三角板重叠部分(阴影部分)的面积为3-$\frac{\sqrt{3}}{6}$.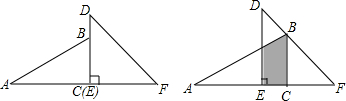
分析 根据特殊角的锐角三角函数值,求出EC、EG、AE的长,得到阴影部分的面积.
解答 解:∵∠F=45°,BC=3,
∴CF=3,又EF=4,
则EC=1,
∵BC=3,∠A=30°,
∴AC=3$\sqrt{3}$,
则AE=3$\sqrt{3}$-1,∠A=30°,
∴EG=3-$\frac{\sqrt{3}}{3}$,
阴影部分的面积为:$\frac{1}{2}$×3$\sqrt{3}$×3-$\frac{1}{2}$×(3$\sqrt{3}$-1)×(3-$\frac{\sqrt{3}}{3}$)
=3-$\frac{\sqrt{3}}{6}$.
故答案为:3-$\frac{\sqrt{3}}{6}$.
点评 本题考查的是平移的性质,正确运用锐角三角函数和特殊角的三角函数值是解题的关键.

练习册系列答案
相关题目
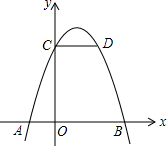 如图,在平面直角坐标系中,抛物线y=a(x-1)2+k(a、k为常数)与x轴交于点A、B,与y轴交于点C,CD∥x轴,与抛物线交于点D.若点A的坐标为(-1,0),则线段OB与线段CD的长度和为5.
如图,在平面直角坐标系中,抛物线y=a(x-1)2+k(a、k为常数)与x轴交于点A、B,与y轴交于点C,CD∥x轴,与抛物线交于点D.若点A的坐标为(-1,0),则线段OB与线段CD的长度和为5.
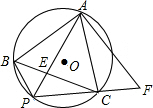 如图,正三角形ABC内接于⊙O,P是BC上的一点,且PB<PC,PA交BC于E,点F是PC延长线上的点,CF=PB,AB=$\sqrt{13}$,PA=4.
如图,正三角形ABC内接于⊙O,P是BC上的一点,且PB<PC,PA交BC于E,点F是PC延长线上的点,CF=PB,AB=$\sqrt{13}$,PA=4.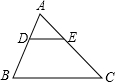 如图,在△ABC中,$\frac{AD}{DB}$=$\frac{AE}{EC}$=$\frac{1}{2}$,若△ADE的面积为1,则四边形DBCE的面积为( )
如图,在△ABC中,$\frac{AD}{DB}$=$\frac{AE}{EC}$=$\frac{1}{2}$,若△ADE的面积为1,则四边形DBCE的面积为( ) 点M是直线y=2x+3上的动点,过点M作MN⊥x轴于点N,当点M位于第二象限时,在y轴上有一点P,使△MNP为等腰直角三角形,则点P的坐标为(0,1)、(0,0)、(0,$\frac{3}{4}$).
点M是直线y=2x+3上的动点,过点M作MN⊥x轴于点N,当点M位于第二象限时,在y轴上有一点P,使△MNP为等腰直角三角形,则点P的坐标为(0,1)、(0,0)、(0,$\frac{3}{4}$). 如图,已知∠BAP与∠APD互补,∠1=∠2,在括号中填上理由.
如图,已知∠BAP与∠APD互补,∠1=∠2,在括号中填上理由.