题目内容
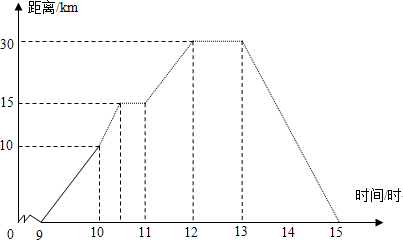
11.小明某天上午9时骑自行车离开家,15时回家,他离家的距离与时间的变化情况如图(1)图象表示变量路程 和时间 的关系;时间是自变量,路程是因变量.
(2)10时,他距离家10 km,13时他距离家30 km.
(3)他到达离家最远的地方是12 时,距离30 km.
(4)11时到12时他行驶了15 km.
(5)他由离家最远的地方返回的平均速度是多少?
分析 (1)根据观察函数图象,可得自变量、因变量,根据路程随时间的变化而变化,可得答案;
(2)根据函数图象的纵坐标,可得离家的距离,根据函数图象的横坐标,可得离家的时间;
(3)根据函数图象的纵坐标,可得离家最远距离,根据函数图象的横坐标,可得离家最远时间;
(4)根据函数图象的纵坐标,可得11时、12时离家的距离,根据有理数的减法,可得答案;
(5)根据函数图象的纵坐标,可得离家最远时间,根据函数图象的横坐标,可得返回的时间,根据路程与时间的关系,可得答案.
解答 解:(1)图象表示变量 路程 和 时间 的关系; 时间是自变量,路程是因变量,
故答案为:路程;时间;时间;距离;
(2)10时,他距离家 10 km,13时他距离家 30 km,
故答案为:10;30;
(3)他到达离家最远的地方是 12 时,距离 30 km,
故答案为:12,30;
(4)11时到12时他行驶了 15 km,
故答案为:15;
(5)他由离家最远的地方返回的平均速度是30÷(15-13)=15(km/h).
点评 本题考查了函数图象,观察函数图象的纵坐标得出路程,函数图象的横坐标得出时间是解题关键.

练习册系列答案
相关题目
2.下列运算正确的是( )
| A. | a+a2=2a3 | B. | a2•a3=a6 | C. | (a2)3=a5 | D. | a6÷a3=a3 |
16.如果三角形的两边长分别为4和5,第三边的长是整数,而且是奇数,则第三边的长可以是( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
 如图,AB⊥CD,垂足为O,EF经过点O,∠1=29°.求∠2和∠3的度数.
如图,AB⊥CD,垂足为O,EF经过点O,∠1=29°.求∠2和∠3的度数.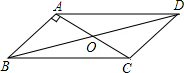 如图,在?ABCD中,对角线AC,BD交于点O,AB⊥AC,∠DAC=45°,AC=2,求BD的长.
如图,在?ABCD中,对角线AC,BD交于点O,AB⊥AC,∠DAC=45°,AC=2,求BD的长.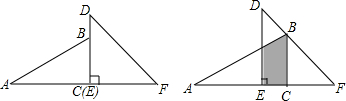
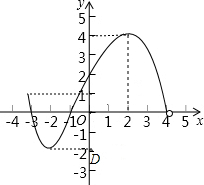 观察图,回答下列问题:
观察图,回答下列问题: