题目内容
15.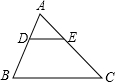 如图,在△ABC中,$\frac{AD}{DB}$=$\frac{AE}{EC}$=$\frac{1}{2}$,若△ADE的面积为1,则四边形DBCE的面积为( )
如图,在△ABC中,$\frac{AD}{DB}$=$\frac{AE}{EC}$=$\frac{1}{2}$,若△ADE的面积为1,则四边形DBCE的面积为( )| A. | 3 | B. | 5 | C. | 7 | D. | 8 |
分析 根据相似三角形的判定推出△ADE∽△ABC,推出$\frac{{S}_{△ADE}}{S△ABC}$=${(\frac{AD}{AB})}^{2}$=$\frac{1}{9}$,求出△ADE的面积即可.
解答 解:∵$\frac{AD}{DB}$=$\frac{AE}{EC}$=$\frac{1}{2}$,
∴DE∥BC,
∴△ADE∽△ABC,
∴$\frac{{S}_{△ADE}}{S△ABC}$=${(\frac{AD}{AB})}^{2}$=$\frac{1}{9}$,
∵△ABC的面积为9,
∴△ADE的面积是1,
∴四边形DBCE的面积是9-1=8,
故选D.
点评 本题考查了相似三角形的性质和判定的应用,熟练地运用性质进行推理是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.甲乙两艘客轮同时离开港口,航行的速度都是每分钟40m,甲客轮用15分钟到达点A,乙客轮用20分钟到达点B,若A、B两点的直线距离为1000m,甲客轮沿着北偏东30°的方向航行,则乙客轮的航行方向可能是( )
| A. | 南偏东60° | B. | 南偏西60° | C. | 北偏西30° | D. | 南偏西30° |
5.下列所学过的真命题中,是公理的是( )
| A. | 对顶角相等 | B. | 同位角相等,两直线平行 | ||
| C. | 三角形两边之和大于第三边 | D. | 同角的余角相等 |
 如图,AB⊥CD,垂足为O,EF经过点O,∠1=29°.求∠2和∠3的度数.
如图,AB⊥CD,垂足为O,EF经过点O,∠1=29°.求∠2和∠3的度数.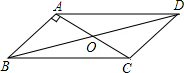 如图,在?ABCD中,对角线AC,BD交于点O,AB⊥AC,∠DAC=45°,AC=2,求BD的长.
如图,在?ABCD中,对角线AC,BD交于点O,AB⊥AC,∠DAC=45°,AC=2,求BD的长. 如图,在△ABC和△DCE中,AB∥DC,AB=DC,BC=CE,且点B,C,E在一条直线上.求证:∠A=∠D.
如图,在△ABC和△DCE中,AB∥DC,AB=DC,BC=CE,且点B,C,E在一条直线上.求证:∠A=∠D.