题目内容
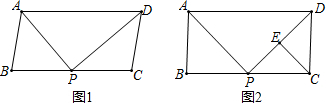
9. 如图,已知∠BAP与∠APD互补,∠1=∠2,在括号中填上理由.
如图,已知∠BAP与∠APD互补,∠1=∠2,在括号中填上理由.∵∠BAP与∠APD互补已知
∴AB∥CD同旁内角互补两直线平行
∴∠BAP=∠APC两直线平行内错角相等
又∵∠1=∠2已知
所以∠BAP-∠1=∠APC-∠2等式的性质1
即∠3=∠4
∴AE∥PF内错角相等两直线平行
∴∠E=∠F两直线平行内错角相等.
分析 根据已知可得出AB∥CD,进而由∠1=∠2可证得∠3=∠4,故能得出AE∥FP,即能推出要证的结论成立.所填的理由主要根据:同位角相等?两直线平行;内错角相等?两直线平行;同旁内角互补?两直线平行,已知条件及等式的性质填写即可.
解答 解:∵∠BAP与∠APD互补(已知)
∴AB∥CD(同旁内角互补,两直线平行)
∴∠BAP=∠APC(两直线平行,内错角相等)
又∵∠1=∠2(已知)
∴∠BAP-∠1=∠APC-∠2(等式的性质1)
即∠3=∠4
∴AE∥PF(内错角相等,两直线平行 )
∴∠E=∠F(两直线平行,内错角相等).
故答案为:已知;同旁内角互补,两直线平行;两直线平行,内错角相等;已知;等式性质1;内错角相等,两直线平行;两直线平行,内错角相等.
点评 本题考查了平行线的性质与判定,正确熟记平行线的判定和性质是解答本题的关键.

练习册系列答案
相关题目
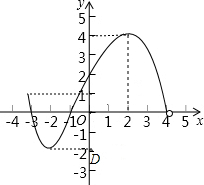 观察图,回答下列问题:
观察图,回答下列问题: