题目内容
10.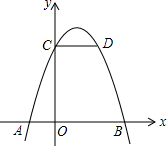 如图,在平面直角坐标系中,抛物线y=a(x-1)2+k(a、k为常数)与x轴交于点A、B,与y轴交于点C,CD∥x轴,与抛物线交于点D.若点A的坐标为(-1,0),则线段OB与线段CD的长度和为5.
如图,在平面直角坐标系中,抛物线y=a(x-1)2+k(a、k为常数)与x轴交于点A、B,与y轴交于点C,CD∥x轴,与抛物线交于点D.若点A的坐标为(-1,0),则线段OB与线段CD的长度和为5.
分析 首先求出抛物线y=a(x-1)2+k(a、k为常数)的对称轴,然后根据A和B、C和D均关于对称轴直线x=1对称,分别求出B和D点的坐标,即可求出OB和CD的长.
解答 解:∵抛物线y=a(x-1)2+k(a、k为常数),
∴对称轴为直线x=1,
∵点A和点B关于直线x=1对称,且点A(-1,0),
∴点B(3,0),
∴OB=3,
∵C点和D点关于x=1对称,且点C(0,a+k),
∴点D(2,a+k),
∴CD=2,
∴线段OB与线段CD的长度和为5,
故答案为5.
点评 本题主要考查了抛物线与x轴交点的知识,解答本题的关键求出抛物线y=a(x-1)2+k(a、k为常数)的对称轴为x=1,此题难度不大.

练习册系列答案
相关题目
5.甲乙两艘客轮同时离开港口,航行的速度都是每分钟40m,甲客轮用15分钟到达点A,乙客轮用20分钟到达点B,若A、B两点的直线距离为1000m,甲客轮沿着北偏东30°的方向航行,则乙客轮的航行方向可能是( )
| A. | 南偏东60° | B. | 南偏西60° | C. | 北偏西30° | D. | 南偏西30° |
15. 小亮从家步行到公交车站台,等公交车去学校.图中的折线表示小亮的行程 s(km)与所花时间t(min)之间的关系.则小亮步行的速度和乘公交车的速度分别是( )
小亮从家步行到公交车站台,等公交车去学校.图中的折线表示小亮的行程 s(km)与所花时间t(min)之间的关系.则小亮步行的速度和乘公交车的速度分别是( )
 小亮从家步行到公交车站台,等公交车去学校.图中的折线表示小亮的行程 s(km)与所花时间t(min)之间的关系.则小亮步行的速度和乘公交车的速度分别是( )
小亮从家步行到公交车站台,等公交车去学校.图中的折线表示小亮的行程 s(km)与所花时间t(min)之间的关系.则小亮步行的速度和乘公交车的速度分别是( )| A. | 100m/min,266m/min | B. | 62.5m/min,500m/min | ||
| C. | 62.5m/min,437.5m/min | D. | 100m/min,500m/min |
2.下列运算正确的是( )
| A. | a+a2=2a3 | B. | a2•a3=a6 | C. | (a2)3=a5 | D. | a6÷a3=a3 |
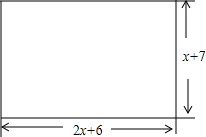 一个工程队要在一块长方形荒地上建造一套简易住房,如图所示,该住房的平面是由长2x+6、宽x+7构成,要求建成:两室、一厅、一厨、一卫,且各房间为长方形或正方形.其中客厅面积为x2+8x+16,厨房面积为3x+6,卫生间面积为x2+3x+2,两个卧室的面积均为3x+9.若墙体所占面积忽略不计,请你根据所学知识,在所给图中设计一套住房的平面结构示意图.(要求:①在图上标出图中各房间的名称;②在图上用含有x的代数式表示图中各房间的边长)
一个工程队要在一块长方形荒地上建造一套简易住房,如图所示,该住房的平面是由长2x+6、宽x+7构成,要求建成:两室、一厅、一厨、一卫,且各房间为长方形或正方形.其中客厅面积为x2+8x+16,厨房面积为3x+6,卫生间面积为x2+3x+2,两个卧室的面积均为3x+9.若墙体所占面积忽略不计,请你根据所学知识,在所给图中设计一套住房的平面结构示意图.(要求:①在图上标出图中各房间的名称;②在图上用含有x的代数式表示图中各房间的边长)