题目内容
5. 点M是直线y=2x+3上的动点,过点M作MN⊥x轴于点N,当点M位于第二象限时,在y轴上有一点P,使△MNP为等腰直角三角形,则点P的坐标为(0,1)、(0,0)、(0,$\frac{3}{4}$).
点M是直线y=2x+3上的动点,过点M作MN⊥x轴于点N,当点M位于第二象限时,在y轴上有一点P,使△MNP为等腰直角三角形,则点P的坐标为(0,1)、(0,0)、(0,$\frac{3}{4}$).
分析 首先根据题意,判断出△MNP为等腰直角三角形的三种情况:(1)两条直角边是MN、MP;(2)两条直角边是MN、NP;(3)两条直角边是MP、NP;然后分类讨论,根据等腰直角三角形的两条直角边相等,以及M是直线y=2x+3上的动点,分别求出点P的坐标各是多少即可.
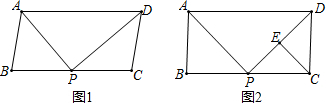
解答 解:(1)如图1,当等腰直角三角形的两条直角边是MN、MP时,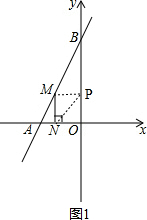 ,
,
设点P的坐标为(0,a),
则点M的坐标为(-a,a),
因为点M是直线y=2x+3上的动点,
所以a=2×(-a)+3,
解得a=1,
所以点P的坐标为(0,1);
(2)如图2,当等腰直角三角形的两条直角边是MN、NP时,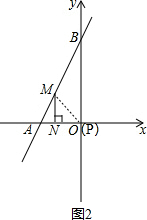 ,
,
点P的坐标为(0,0),
则点M的坐标为(-b,b),
因为点M是直线y=2x+3上的动点,
所以b=2×(-b)+3,
解得b=1,
即点M的坐标为(-1,1),点N的坐标为(-1,0),点P的坐标为(0,0);
(3)如图3,当等腰直角三角形的两条直角边是MP、NP时,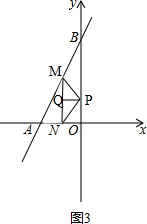 ,
,
作PQ⊥MN交MN与点Q,
设点P的坐标为(0,c),
因为MP=NP,∠MPN=90°,
所以点M的坐标为(-c,2c),
因为点M是直线y=2x+3上的动点,
所以2c=2×(-c)+3,
解得a=$\frac{3}{4}$,
所以点P的坐标为(0,$\frac{3}{4}$);
综上,可得
点P的坐标为(0,1)、(0,0)、(0,$\frac{3}{4}$).
故答案为:(0,1)、(0,0)、(0,$\frac{3}{4}$).
点评 (1)此题主要考查了一次函数综合题,考查了分析推理能力,考查了分类讨论思想的应用,考查了从已知函数图象中获取信息,并能利用获取的信息解答相应的问题的能力;解答此题的关键是判断出△MNP为等腰直角三角形的三种情况:(1)两条直角边是MN、MP;(2)两条直角边是MN、NP;(3)两条直角边是MP、NP.
(2)此题还考查了等腰直角三角形的性质,要熟练掌握.

 口算题天天练系列答案
口算题天天练系列答案 小亮从家步行到公交车站台,等公交车去学校.图中的折线表示小亮的行程 s(km)与所花时间t(min)之间的关系.则小亮步行的速度和乘公交车的速度分别是( )
小亮从家步行到公交车站台,等公交车去学校.图中的折线表示小亮的行程 s(km)与所花时间t(min)之间的关系.则小亮步行的速度和乘公交车的速度分别是( )| A. | 100m/min,266m/min | B. | 62.5m/min,500m/min | ||
| C. | 62.5m/min,437.5m/min | D. | 100m/min,500m/min |
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
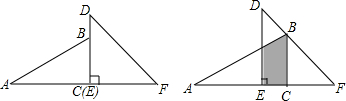
 如图,点A为一次函数y=-x+5与反比例函数y=$\frac{2}{x}$图象的一个交点,AB⊥y轴于点B,AC⊥x轴于点C,则矩形ABOC的面积为多少?周长为多少?
如图,点A为一次函数y=-x+5与反比例函数y=$\frac{2}{x}$图象的一个交点,AB⊥y轴于点B,AC⊥x轴于点C,则矩形ABOC的面积为多少?周长为多少?