题目内容
12.在平面直角坐标系中,O为坐标原点,已知点P的坐标为(3,m),连接OP,OP=5,将线段OP绕O点顺时针旋转90°得OP1,则点P1的坐标为(4,-3)或(-4,-3).分析 先由点P的坐标为(3,m),OP=5,利用勾股定理求出点P的纵坐标为4或-4,再抓住旋转的三要素:旋转中心是O,旋转方向顺时针,旋转角度90°,通过画图得出点P1的坐标.
解答  解:∵点P的坐标为(3,m),OP=5,
解:∵点P的坐标为(3,m),OP=5,
∴|m|=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴m=4或-4,
如图,若点P的坐标为(3,4),则点P1的坐标为(4,-3),
若点P的坐标为(3,-4),则点P1的坐标为(-4,-3),
所以,点P1的坐标为(4,-3)或(-4,-3).
故答案为:(4,-3)或(-4,-3).
点评 本题考查了坐标与图形变换-旋转,勾股定理,能正确画出图形是解此题的关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
4.已知点A的坐标为(a,b),O为坐标原点,连结OA,将线段OA绕点O按逆时针方向旋转180°得OA1,则点A1的坐标为( )
| A. | (-a,b) | B. | (a,-b) | C. | (-a,-b) | D. | (b,-a) |
2.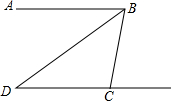 如图,AB∥CD,BD平分∠ABC,若∠DCB=100°,则∠D的度数是( )
如图,AB∥CD,BD平分∠ABC,若∠DCB=100°,则∠D的度数是( )
 如图,AB∥CD,BD平分∠ABC,若∠DCB=100°,则∠D的度数是( )
如图,AB∥CD,BD平分∠ABC,若∠DCB=100°,则∠D的度数是( )| A. | 40° | B. | 50° | C. | 30° | D. | 45° |

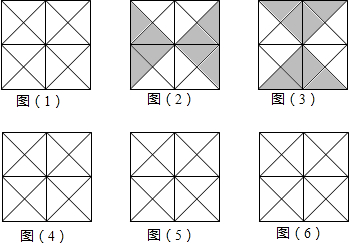
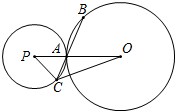 如图,已知⊙O的半径为5,⊙P与⊙O外切于点A,经过点A的直线与⊙O、⊙P分别交于点B、C,tan∠OAB=$\frac{\sqrt{21}}{2}$.
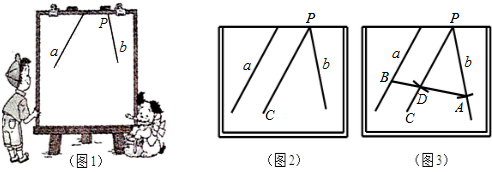
如图,已知⊙O的半径为5,⊙P与⊙O外切于点A,经过点A的直线与⊙O、⊙P分别交于点B、C,tan∠OAB=$\frac{\sqrt{21}}{2}$.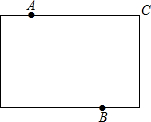 某地拟在新竣工的矩形广场的内部修建一个音乐喷泉,要求音乐喷泉P到广场的两个入口A、B的距离相等,且到广场管理处C的距离等于A和B之间距离的一半,A、B、C的位置如图所示.请利用尺规作图作出音乐喷泉P的位置.(要求:不写作法,但要保留作图痕迹,必须用铅笔作图).
某地拟在新竣工的矩形广场的内部修建一个音乐喷泉,要求音乐喷泉P到广场的两个入口A、B的距离相等,且到广场管理处C的距离等于A和B之间距离的一半,A、B、C的位置如图所示.请利用尺规作图作出音乐喷泉P的位置.(要求:不写作法,但要保留作图痕迹,必须用铅笔作图).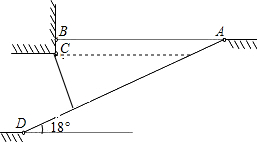 为缓解实验北校“停车难”问题,现计划拟建造地下停车库,建筑师提供了地下停车库的设计示意图,按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入,其中AB=10m,BC=0.5m,为在入口标明限高,请你根据该图计算出停车库的限高.(精确到0.1m)
为缓解实验北校“停车难”问题,现计划拟建造地下停车库,建筑师提供了地下停车库的设计示意图,按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入,其中AB=10m,BC=0.5m,为在入口标明限高,请你根据该图计算出停车库的限高.(精确到0.1m)