题目内容
7.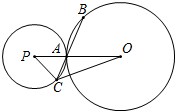 如图,已知⊙O的半径为5,⊙P与⊙O外切于点A,经过点A的直线与⊙O、⊙P分别交于点B、C,tan∠OAB=$\frac{\sqrt{21}}{2}$.
如图,已知⊙O的半径为5,⊙P与⊙O外切于点A,经过点A的直线与⊙O、⊙P分别交于点B、C,tan∠OAB=$\frac{\sqrt{21}}{2}$.(1)求AB的长;
(2)当∠OCA=∠OPC时,求⊙P的半径.
分析 (1)作OM⊥AB于M,如图,在Rt△OAM中根据正切定义得到tan∠OAM=$\frac{OM}{AM}$=$\frac{\sqrt{21}}{2}$,则设OM=$\sqrt{21}$x,AM=2x,由勾股定理得OA=5x,所以5x=5,解得x=1,于是得到AM=2,OM=$\sqrt{21}$,然后根据垂径定理得到AB=2AM=4;
(2)作PN⊥AC于N,如图,则AN=CN,设⊙P的半径为r,先证明△PAN∽△OAM,利用相似比得到AN=$\frac{2}{5}$r,则AC=2AN=$\frac{4}{5}$r,在Rt△OMC中,根据勾股定理得到OC2($\sqrt{21}$)2+($\frac{4}{5}$r+2)2,再证明∴△OAC∽△OCP,利用相似比得到OC2=OA•OP=5(5+r),则($\sqrt{21}$)2+($\frac{4}{5}$r+2)2=5(5+r),然后解r的方程即可.
解答 解:(1) 作OM⊥AB于M,如图,
作OM⊥AB于M,如图,
在Rt△OAM中,tan∠OAM=$\frac{OM}{AM}$=$\frac{\sqrt{21}}{2}$,
设OM=$\sqrt{21}$x,AM=2x,
∴OA=$\sqrt{O{M}^{2}+A{M}^{2}}$=5x,
∴5x=5,解得x=1,
∴AM=2,OM=$\sqrt{21}$,
∵OM⊥AB,
∴AM=BM,
∴AB=2AM=4;
(2)作PN⊥AC于N,如图,则AN=CN,设⊙P的半径为r,
∵OM∥AN,
∴△PAN∽△OAM,
∴$\frac{PA}{OA}$=$\frac{AN}{AM}$,即$\frac{r}{5}$=$\frac{AN}{2}$,解得AN=$\frac{2}{5}$r,
∴AC=2AN=$\frac{4}{5}$r,
∴MC=AC+AM=$\frac{4}{5}$r+2,
在Rt△OMC中,OC2=OM2+MC2=($\sqrt{21}$)2+($\frac{4}{5}$r+2)2,
∵∠OCA=∠OPC,
而∠AOC=∠COP,
∴△OAC∽△OCP,
∴OC:OP=OA:OC,
∴OC2=OA•OP=5(5+r),
∴($\sqrt{21}$)2+($\frac{4}{5}$r+2)2=5(5+r),
整理得16r2-45r=0,解得r1=0(舍去),r2=$\frac{45}{16}$,
即⊙P的半径为$\frac{45}{16}$.
点评 本题考查了相切两圆的性质:如果两圆相切,那么连心线必经过切点.也考查了垂径定理、相似三角形的判定与性质和解直角三角形.

| A. | (3,-4) | B. | (2,-3) | C. | (-3,2) | D. | (4,-3) |
| A. | 9.7×10-7 | B. | 97×10-7 | C. | 0.97×10-7 | D. | 9.7×10-8 |
 如图,D是△ABC的边AB上的一点,过点D作DE∥BC交AC于E,若AD:BD=4:3,则S△ADE:S△ABC=16:49.
如图,D是△ABC的边AB上的一点,过点D作DE∥BC交AC于E,若AD:BD=4:3,则S△ADE:S△ABC=16:49.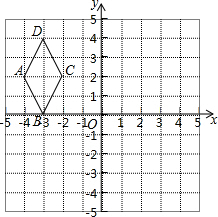 下面方格中有一个菱形ABCD和点O,请你在方格中画出以下图形(只要求画出平移、旋转后的图形,不要求写出作图步骤和过程).
下面方格中有一个菱形ABCD和点O,请你在方格中画出以下图形(只要求画出平移、旋转后的图形,不要求写出作图步骤和过程).
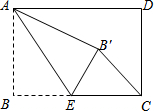 如图,长方形的宽AB=3,长BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处.
如图,长方形的宽AB=3,长BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处.