题目内容
10．
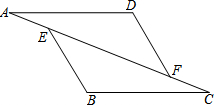如图，已知：在△AFD和△CEB中，点A、E、F、C在同一直线上，AE=CF，AD∥BC，AD=BC．求证：BE∥DF．
分析 欲证明BE∥DF，只要证明∠AFD=∠BEC，只要证明△ADF≌△CBE即可．
解答 证明：∵AD∥BC，
∴∠A=∠C，
∵AE=CF，
∴AE+EF=CF+EF，
即AF=EC，
在△ADF和△CBE中，
$\left\{\begin{array}{l}{AD=BC}\\{∠A=∠C}\\{AF=CE}\end{array}\right.$，
∴△ADF≌△CBE，
∴∠AFD=∠BEC，
∴BE∥DF．
点评 本题考查全等三角形的判定和性质、平行线的性质和判定等知识，解题的关键是正确寻找全等三角形，属于基础题，中考常考题型．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
1．下列判断错误的是（ ）
| A． | 当a≠0时，分式$\frac{2}{a}$有意义 | B． | 当a=-3时，分式$\frac{a+3}{{{a^2}-9}}$有意义 | ||
| C． | 当$a=-\frac{1}{2}$时，分式$\frac{2a+1}{a}$的值为0 | D． | 当a=1时，分式$\frac{2a-1}{a}$的值为1 |
18．
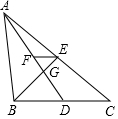如图，△ABC的两条中线AD和BE相交于点G，过点E作EF∥BC交AD于点F，则FG：AG是（ ）
如图，△ABC的两条中线AD和BE相交于点G，过点E作EF∥BC交AD于点F，则FG：AG是（ ）| A． | 1：4 | B． | 1：3 | C． | 1：2 | D． | 2：3 |
5．
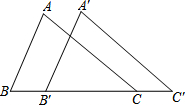如图，在△ABC中，AB=8，BC=12，∠B=60°，将△ABC沿着射线BC的方向平移4个单位后，得到△A'B'C'，连接AC，则△A'B'C的面积是（ ）
如图，在△ABC中，AB=8，BC=12，∠B=60°，将△ABC沿着射线BC的方向平移4个单位后，得到△A'B'C'，连接AC，则△A'B'C的面积是（ ）| A． | 16 | B． | $4\sqrt{3}$ | C． | $16\sqrt{3}$ | D． | $32\sqrt{3}$ |
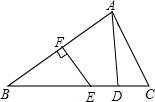如图，在△ABC中，AB的垂直平分线EF交BC于点E，交AB于点F，D为线段CE的中点，BE=AC．