题目内容
18．
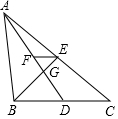如图，△ABC的两条中线AD和BE相交于点G，过点E作EF∥BC交AD于点F，则FG：AG是（ ）| A． | 1：4 | B． | 1：3 | C． | 1：2 | D． | 2：3 |
分析 根据重心的性质得到AG=2DG，BG=2GE，根据平行线分线段成比例定理计算即可．
解答 解：∵△ABC的两条中线AD和BE相交于点G，
∴点G是△ABC的重心，
∴AG=2DG，BG=2GE，
∵EF∥BC，
∴$\frac{FG}{GD}$=$\frac{EG}{GB}$=$\frac{1}{2}$，
∴FG：AG=1：4，
故选：A．
点评 本题考查的是三角形的重心的概念和性质、平行线分线段成比例定理的应用，三角形的重心是三角形三条中线的交点，且重心到顶点的距离是它到对边中点的距离的2倍．
练习册系列答案
相关题目
如图所示的几何体是由9个小正方体组合而成的，它的左视图是（ ）
9．计算-2x（x2-1）的结果是（ ）
| A． | -2x3-2x | B． | -2x3+x | C． | -2x3+2x | D． | -x3+2x |
13．下列说法错误的是（ ）
| A． | 过一点能作无数条直线 | |
| B． | 连接两点之间的线段就是两点间的距离 | |
| C． | 反向延长线段AB和延长线段BA是一回事 | |
| D． | 两点确定一条直线 |
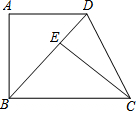如图，在四边形ABCD中，AD∥BC，∠A=90°，CE⊥BD于E，AB=EC．
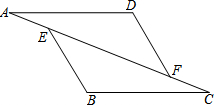如图，已知：在△AFD和△CEB中，点A、E、F、C在同一直线上，AE=CF，AD∥BC，AD=BC．求证：BE∥DF．
7．已知反比例函数y=-$\frac{8}{x}$，则下列各点在此函数图象上的是（ ）
| A． | （2，4） | B． | （-1，-8） | C． | （-2，-4） | D． | （4，-2） |