题目内容
20.当x分别取2016、2015、2014…、2、1、1、$\frac{1}{2}$、$\frac{1}{3}$、…、$\frac{1}{2014}$、$\frac{1}{2015}$、$\frac{1}{2016}$时,计算分式$\frac{{x}^{2}-1}{{x}^{2}+1}$的值,再将所得结果相加,其和等于( )| A. | 0 | B. | 1 | C. | -1 | D. | 2014 |
分析 设a为负整数,将x=a代入得:$\frac{{a}^{2}-1}{{a}^{2}+1}$,将x=-$\frac{1}{a}$代入得:$\frac{(-\frac{1}{a})^{2}-1}{(-\frac{1}{a})^{2}+1}$=$\frac{\frac{1-{a}^{2}}{{a}^{2}}}{\frac{{a}^{2}+1}{{a}^{2}}}$=$\frac{1-{a}^{2}}{{a}^{2}+1}$,故此可知当x互为负倒数时,两分式的和为0,然后求得分式的值即可.
解答 解:∵将x=a代入得:$\frac{{a}^{2}-1}{{a}^{2}+1}$,将x=-$\frac{1}{a}$代入得:$\frac{(-\frac{1}{a})^{2}-1}{(-\frac{1}{a})^{2}+1}$=$\frac{\frac{1-{a}^{2}}{{a}^{2}}}{\frac{{a}^{2}+1}{{a}^{2}}}$=$\frac{1-{a}^{2}}{{a}^{2}+1}$,
∴$\frac{{a}^{2}-1}{{a}^{2}+1}$+$\frac{1-{a}^{2}}{{a}^{2}+1}$=0,
故当x分别取2016、2015、2014…、2、1、1、$\frac{1}{2}$、$\frac{1}{3}$、…、$\frac{1}{2014}$、$\frac{1}{2015}$、$\frac{1}{2016}$时,得出分式$\frac{{x}^{2}-1}{{x}^{2}+1}$的值,再将所得结果相加,其和等于:0.
故选:A.
点评 本题主要考查的是分式的加减,发现当x的值互为负倒数时,两分式的和为0是解题的关键.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
9.计算-2x(x2-1)的结果是( )
| A. | -2x3-2x | B. | -2x3+x | C. | -2x3+2x | D. | -x3+2x |
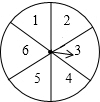 转盘被划分成六个相同大小的扇形,并分别标上1,2,3,4,5,6这六个数字,指针停在每个扇形的可能性相等.四位同学各自发表了下述见解:
转盘被划分成六个相同大小的扇形,并分别标上1,2,3,4,5,6这六个数字,指针停在每个扇形的可能性相等.四位同学各自发表了下述见解: 如图,AB为⊙O的直径,弦CD⊥AB于H,E为AB延长线上一点,CE交⊙O于点F
如图,AB为⊙O的直径,弦CD⊥AB于H,E为AB延长线上一点,CE交⊙O于点F 如图所示的几何体是由9个小正方体组合而成的,它的左视图是( )
如图所示的几何体是由9个小正方体组合而成的,它的左视图是( )



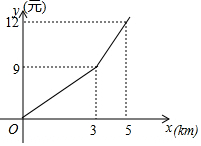 某出租车公司的收费标准如图,其中x(km)表示行驶里程,y(元)表示车费,若乘客在打车后付费42元,则该乘客乘坐出租车行驶了25km.
某出租车公司的收费标准如图,其中x(km)表示行驶里程,y(元)表示车费,若乘客在打车后付费42元,则该乘客乘坐出租车行驶了25km.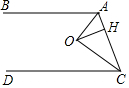 如图,AB∥CD,OA,OC分别平分∠BAC和∠ACD,OH⊥AC于点H,且OH=4,则AB,CD之间的距离为8.
如图,AB∥CD,OA,OC分别平分∠BAC和∠ACD,OH⊥AC于点H,且OH=4,则AB,CD之间的距离为8.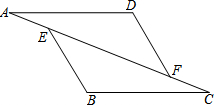 如图,已知:在△AFD和△CEB中,点A、E、F、C在同一直线上,AE=CF,AD∥BC,AD=BC.求证:BE∥DF.
如图,已知:在△AFD和△CEB中,点A、E、F、C在同一直线上,AE=CF,AD∥BC,AD=BC.求证:BE∥DF.