题目内容
20.平面直角坐标系中,我们把点P(x,y)的横坐标与纵坐标的绝对值之和叫做点P(x,y)的勾股值,记为:「P」,即「P」=|x|+|y|.(1)求点A(-1,3)的勾股值「A」;
(2)若点B在第一象限且满足「B」=3,求满足条件的所有B点与坐标轴围成的图形的面积.
分析 (1)由勾股值的定义即可求解;
(2)设B点的坐标为(x,y),由「B」=3,得到方程|x|+|y|=3,得到x+y=3,-x-y=3,x-y=3,-x+y=3,化为一次函数的解析式y=-x+3,y=-x-3,y=x-3,y=x+3,于是得到所有点N围成的图形是边长为3$\sqrt{2}$的正方形,则面积可求.
解答 解:(1)「A」=|-1|+|3|=4,
(2)设B(x,y),由「B」=3且在第一象限知,x+y=3(x>0,y>0),
即:y=-x+3(x>0,y>0).
故所有点B与坐标轴围成的图形如图所示的三角形,
故其面积为$\frac{1}{2}$×3×3=$\frac{9}{2}$.
点评 本题考查了坐标与图形的性质,正确理解勾股值的定义是解题的关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
9.小强是一位密码编译爱好者,在他的密码手册中,有这样一条信息,a-b,x-y,x+y,a+b,x2-y2,a2-b2分别对应下列六个字:台、爱、我、邢、游、美,现将(x2-y2)a2-(x2-y2)b2因式分解,结果呈现的密码信息可能是( )
| A. | 我爱美 | B. | 邢台游 | C. | 爱我邢台 | D. | 美我邢台 |
10. 如图,在?ABCD中,点E是边AD的中点,EC交对角线BD于点F,则DF:BD等于( )
如图,在?ABCD中,点E是边AD的中点,EC交对角线BD于点F,则DF:BD等于( )
 如图,在?ABCD中,点E是边AD的中点,EC交对角线BD于点F,则DF:BD等于( )
如图,在?ABCD中,点E是边AD的中点,EC交对角线BD于点F,则DF:BD等于( )| A. | 1:3 | B. | 3:1 | C. | 2:1 | D. | 1:2 |
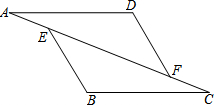 如图,已知:在△AFD和△CEB中,点A、E、F、C在同一直线上,AE=CF,AD∥BC,AD=BC.求证:BE∥DF.
如图,已知:在△AFD和△CEB中,点A、E、F、C在同一直线上,AE=CF,AD∥BC,AD=BC.求证:BE∥DF.