题目内容
5.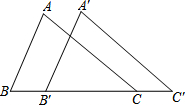 如图,在△ABC中,AB=8,BC=12,∠B=60°,将△ABC沿着射线BC的方向平移4个单位后,得到△A'B'C',连接AC,则△A'B'C的面积是( )
如图,在△ABC中,AB=8,BC=12,∠B=60°,将△ABC沿着射线BC的方向平移4个单位后,得到△A'B'C',连接AC,则△A'B'C的面积是( )| A. | 16 | B. | $4\sqrt{3}$ | C. | $16\sqrt{3}$ | D. | $32\sqrt{3}$ |
分析 根据平移的性质可得A′B′=AB,∠A′B′C′=∠B,再求出B′C,过点A′作A′D⊥B′C于D,再求出A′D,然后根据三角形的面积公式列式计算即可得解.
解答  解:∵△ABC沿着射线BC的方向平移4个单位后,得到△A′B′C′,
解:∵△ABC沿着射线BC的方向平移4个单位后,得到△A′B′C′,
∴A′B′=AB=8,∠A′B′C′=∠B=60°,
B′C=12-4=8,
过点A′作A′D⊥B′C于D,
则A′D=$\frac{\sqrt{3}}{2}$A′B′=$\frac{\sqrt{3}}{2}$×8=4$\sqrt{3}$,
∴△A′B′C的面积=$\frac{1}{2}$B′C•A′D=$\frac{1}{2}$×8×4$\sqrt{3}$=16$\sqrt{3}$.
故选C.
点评 本题考查平移的基本性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.

练习册系列答案
相关题目
13.下列说法错误的是( )
| A. | 过一点能作无数条直线 | |
| B. | 连接两点之间的线段就是两点间的距离 | |
| C. | 反向延长线段AB和延长线段BA是一回事 | |
| D. | 两点确定一条直线 |
20.为庆祝交通大学建校120周年,我校特别推出校庆纪念卡片,卡片有两种,一种卡片正面印着交通大学的校训,另一种卡片正面印着交通大学的校徽,两种卡片除此之外完全相同.现将3张校训卡和4张校徽正面向下放置在桌面上,随机翻出4张卡片.则下列事件是必然事件的是( )
| A. | 至少有一张是校训卡 | B. | 至少有一张是校徽卡 | ||
| C. | 翻出的卡既有校训卡又有校徽卡 | D. | 发出的卡片只有一种类型 |
17.如果一个角的补角是150°,那么这个角的余角的度数是( )
| A. | 60° | B. | 30° | C. | 90° | D. | 120° |
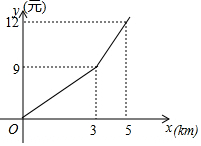 某出租车公司的收费标准如图,其中x(km)表示行驶里程,y(元)表示车费,若乘客在打车后付费42元,则该乘客乘坐出租车行驶了25km.
某出租车公司的收费标准如图,其中x(km)表示行驶里程,y(元)表示车费,若乘客在打车后付费42元,则该乘客乘坐出租车行驶了25km. 如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,如果BD=12cm,那么CD的长应为6cm;点D到AB的距离是6cm.
如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,如果BD=12cm,那么CD的长应为6cm;点D到AB的距离是6cm.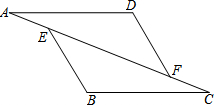 如图,已知:在△AFD和△CEB中,点A、E、F、C在同一直线上,AE=CF,AD∥BC,AD=BC.求证:BE∥DF.
如图,已知:在△AFD和△CEB中,点A、E、F、C在同一直线上,AE=CF,AD∥BC,AD=BC.求证:BE∥DF. 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(3,-1).以原点O为对称中心,画出△ABC关于原点O对称的△A′B′C′,并写出A′、B′、C′的坐标.
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(3,-1).以原点O为对称中心,画出△ABC关于原点O对称的△A′B′C′,并写出A′、B′、C′的坐标.