题目内容
12. 梯形ABCD中,E为BC上一点,且AE=DE;F为AD上一点,且∠AFB=∠DFC.求证:FMEN为平行四边形.
梯形ABCD中,E为BC上一点,且AE=DE;F为AD上一点,且∠AFB=∠DFC.求证:FMEN为平行四边形.
分析 根据等腰三角形的性质得到∠DAE=∠ADE,根据梯形的性质得到AB∥CD,根据平行线的性质得到角的关系,然后根据平行四边形的判定定理即可得到结论.
解答 证明:∵AE=DE,∠AFB=∠DFN,
∴∠DAE=∠ADE,
∵AB∥CD,∠BAD+∠ADC=180°,
∴∠AED=∠BAM+∠NDC,
∵∠FBC+∠BFC+∠BCF=180°,
∵∠ABC+∠DCB=180°,
∴∠BFC=∠ABF+DCF,
∵∠AFB=∠DFC,
∴∠FAB+∠ABF=∠FCD+FDC,
∴∠MAB+∠MBA=∠NCD+∠NDC,
∴∠AMB=∠CND,
∴∠FME=∠ENF,
∵∠BFC=∠ABM+∠DCN,∠AED=∠ABM+∠NDC,∠AMB=∠CND,
∴∠ABM+∠DCN=∠BAM+∠NDC,
∴∠BFC=∠AED,
∴四边形FMEN为平行四边形.
点评 本题考查了平行四边形的判定定理.等腰三角形的性质,相似三角形的性质,证得△AFM∽△ADE∽△FND是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
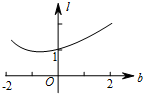
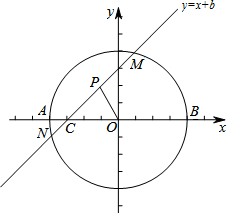 如图在直角坐标系中,已知A(-2,0),B(2,0).直线y=x+b(-2≤b≤2)交x轴于点C,交以AB为直径的⊙O于M,N两点(M在N的上方),点P是MC的中点(当M,C点重合时,点P即是点M).设线段OP的长度为l,则下列图象中大致能表示l与b之间的函数关系的图象是( )
如图在直角坐标系中,已知A(-2,0),B(2,0).直线y=x+b(-2≤b≤2)交x轴于点C,交以AB为直径的⊙O于M,N两点(M在N的上方),点P是MC的中点(当M,C点重合时,点P即是点M).设线段OP的长度为l,则下列图象中大致能表示l与b之间的函数关系的图象是( )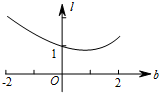


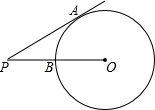 如图,PA为⊙O的切线,切点为A,连接OP交圆于点B,已知PA=4,PB=2,则⊙O的半径为3.
如图,PA为⊙O的切线,切点为A,连接OP交圆于点B,已知PA=4,PB=2,则⊙O的半径为3.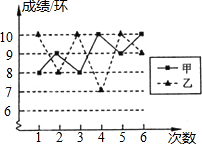 射击队为甲、乙两名运动员中选拨一人参加比赛,对他们进行了六次测试,测试成绩如图.
射击队为甲、乙两名运动员中选拨一人参加比赛,对他们进行了六次测试,测试成绩如图.
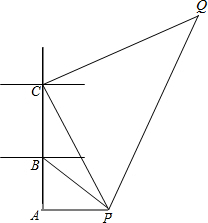 如图,有A,B,C三个港口,都位于南北方向的海岸线上,P、Q是两个度银小岛,某游船从小岛P出发,向西航行到达港口A,再从港口A向北航行,到达港口B,在港口B看到小岛P在南偏东60°处,游船由港口B出发40分钟后到达港口C,看到小岛P在南偏东30°处,这时游船的航向改为北偏东60°继续航行80分钟到达小岛Q.从港口A到小岛Q,该游船航行的速度都有30海里/小时.
如图,有A,B,C三个港口,都位于南北方向的海岸线上,P、Q是两个度银小岛,某游船从小岛P出发,向西航行到达港口A,再从港口A向北航行,到达港口B,在港口B看到小岛P在南偏东60°处,游船由港口B出发40分钟后到达港口C,看到小岛P在南偏东30°处,这时游船的航向改为北偏东60°继续航行80分钟到达小岛Q.从港口A到小岛Q,该游船航行的速度都有30海里/小时.