题目内容
3.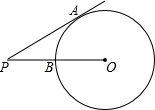 如图,PA为⊙O的切线,切点为A,连接OP交圆于点B,已知PA=4,PB=2,则⊙O的半径为3.
如图,PA为⊙O的切线,切点为A,连接OP交圆于点B,已知PA=4,PB=2,则⊙O的半径为3.
分析 根据题意,连接OA,可知∠OAP=90°,然后根据勾股定理可以求得OA的长,本题得以解决.
解答 解:连接OA,如下图所示,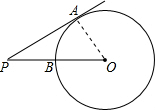
∵PA为⊙O的切线,
∴∠OAP=90°,
设圆的半径为r,
∵PA=4,PB=2,PA2+OA2=OP2,
∴,42+r2=(2+r)2
解得,r=3
故答案为:3.
点评 本题考查切线的性质、勾股定理,解题的关键明确切线的性质,会利用勾股定理求直角三角形的某一边的长.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.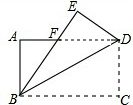 如图,矩形ABCD中,3AB=2AD,沿对角线BD折叠,得△BED,BE与AD交于点F,则$\frac{AF}{FD}$等于( )
如图,矩形ABCD中,3AB=2AD,沿对角线BD折叠,得△BED,BE与AD交于点F,则$\frac{AF}{FD}$等于( )
 如图,矩形ABCD中,3AB=2AD,沿对角线BD折叠,得△BED,BE与AD交于点F,则$\frac{AF}{FD}$等于( )
如图,矩形ABCD中,3AB=2AD,沿对角线BD折叠,得△BED,BE与AD交于点F,则$\frac{AF}{FD}$等于( )| A. | $\frac{2}{5}$ | B. | $\frac{5}{13}$ | C. | $\frac{1}{3}$ | D. | $\frac{2}{7}$ |
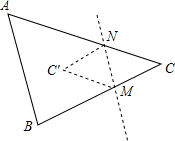 已知,如图,△ABC中,把点C沿直线MN对折得点C′.
已知,如图,△ABC中,把点C沿直线MN对折得点C′.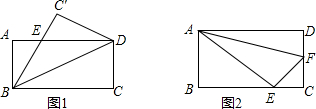
 梯形ABCD中,E为BC上一点,且AE=DE;F为AD上一点,且∠AFB=∠DFC.求证:FMEN为平行四边形.
梯形ABCD中,E为BC上一点,且AE=DE;F为AD上一点,且∠AFB=∠DFC.求证:FMEN为平行四边形.