题目内容
1.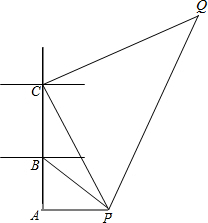 如图,有A,B,C三个港口,都位于南北方向的海岸线上,P、Q是两个度银小岛,某游船从小岛P出发,向西航行到达港口A,再从港口A向北航行,到达港口B,在港口B看到小岛P在南偏东60°处,游船由港口B出发40分钟后到达港口C,看到小岛P在南偏东30°处,这时游船的航向改为北偏东60°继续航行80分钟到达小岛Q.从港口A到小岛Q,该游船航行的速度都有30海里/小时.
如图,有A,B,C三个港口,都位于南北方向的海岸线上,P、Q是两个度银小岛,某游船从小岛P出发,向西航行到达港口A,再从港口A向北航行,到达港口B,在港口B看到小岛P在南偏东60°处,游船由港口B出发40分钟后到达港口C,看到小岛P在南偏东30°处,这时游船的航向改为北偏东60°继续航行80分钟到达小岛Q.从港口A到小岛Q,该游船航行的速度都有30海里/小时.(1)求港口C与小岛P之间的距离;
(2)求P,Q两个小岛之间的距离.($\sqrt{7}$≈2.646,结果精确到十分位).
分析 (1)根据题意确定BC、∠ABP、∠ACP,根据三角形的外角的性质求出∠BPC,根据等腰三角形的性质和正弦的定义计算即可;
(2)根据题意得到∠PCQ=90°,根据勾股定理计算即可.
解答 解:(1)由题意得,BC=30×$\frac{2}{3}$=20海里,∠ABP=60°,∠ACP=30°,
∴∠BPC=30°,
∴BP=BC=20海里,
∴AP=BP•sin∠ABP=20×$\frac{\sqrt{3}}{2}$=10$\sqrt{3}$,
∵∠ACP=30°,
∴PC=2AP=20$\sqrt{3}$海里,
答:港口C与小岛P之间的距离为20$\sqrt{3}$海里;
(2)∵在港口C看到小岛P在南偏东30°处,游船的航向改为北偏东60°,
∴∠PCQ=90°,又CQ=30×$\frac{4}{3}$=40海里,
由勾股定理得,PQ=$\sqrt{C{P}^{2}+C{Q}^{2}}$=20$\sqrt{7}$≈52.9海里,
答:P,Q两个小岛之间的距离约为52.9海里.
点评 本题考查的是解直角三角形的应用-方向角问题,正确标注方向角、熟记锐角三角函数的定义是解题的关键.

练习册系列答案
相关题目
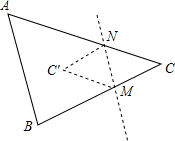 已知,如图,△ABC中,把点C沿直线MN对折得点C′.
已知,如图,△ABC中,把点C沿直线MN对折得点C′. 梯形ABCD中,E为BC上一点,且AE=DE;F为AD上一点,且∠AFB=∠DFC.求证:FMEN为平行四边形.
梯形ABCD中,E为BC上一点,且AE=DE;F为AD上一点,且∠AFB=∠DFC.求证:FMEN为平行四边形.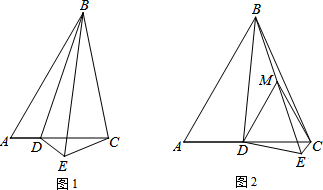
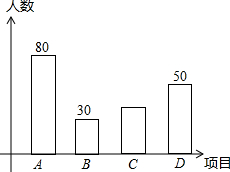 某中学开展“阳光体育一小时”活动.根据学校事假情况,决定开设四项运动项目:A:踢毽子;B:篮球;C:跳绳;D:乒乓球.为了解学生最喜欢哪一种运动项目,随机抽取了n名学生进行问卷调查,每位学生在问卷调查时都按要求只选择了其中一种喜欢的运动项目.收回全部问卷后,将收集到的数据整理并绘制成如下的统计图,若参与调查的学生中喜欢A方式的学生的人数占参与调查学生人数的40%.根据统计图提供的信息,解答下列问题:
某中学开展“阳光体育一小时”活动.根据学校事假情况,决定开设四项运动项目:A:踢毽子;B:篮球;C:跳绳;D:乒乓球.为了解学生最喜欢哪一种运动项目,随机抽取了n名学生进行问卷调查,每位学生在问卷调查时都按要求只选择了其中一种喜欢的运动项目.收回全部问卷后,将收集到的数据整理并绘制成如下的统计图,若参与调查的学生中喜欢A方式的学生的人数占参与调查学生人数的40%.根据统计图提供的信息,解答下列问题: