题目内容
2.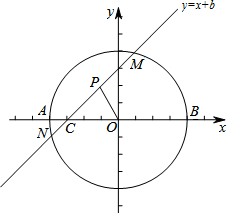 如图在直角坐标系中,已知A(-2,0),B(2,0).直线y=x+b(-2≤b≤2)交x轴于点C,交以AB为直径的⊙O于M,N两点(M在N的上方),点P是MC的中点(当M,C点重合时,点P即是点M).设线段OP的长度为l,则下列图象中大致能表示l与b之间的函数关系的图象是( )
如图在直角坐标系中,已知A(-2,0),B(2,0).直线y=x+b(-2≤b≤2)交x轴于点C,交以AB为直径的⊙O于M,N两点(M在N的上方),点P是MC的中点(当M,C点重合时,点P即是点M).设线段OP的长度为l,则下列图象中大致能表示l与b之间的函数关系的图象是( )| A. | 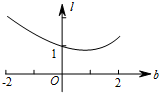 | B. |  | ||
| C. |  | D. | 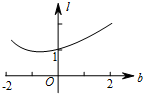 |
分析 求出l与b的关系式即可解决问题.
解答 解:∵点C坐标(-b,0),点M坐标(b,0),
∴OC=OM,
∵OP=PM,∠COM=90°
∴OP⊥CM,OP=PM=CP=$\frac{\sqrt{2}}{2}$OM.
∴l=$\frac{\sqrt{2}}{2}$|b|.
故图象选C.
点评 本题考查动点问题的函数图象、等腰直角三角形的判定和性质等知识,解题关键是列出函数解析式,属于中考常考题型.

练习册系列答案
相关题目
7. 如图,⊙O的弦AB=8,P是劣弧AB中点,连结OP交AB于C,且PC=2,则⊙O的半径为( )
如图,⊙O的弦AB=8,P是劣弧AB中点,连结OP交AB于C,且PC=2,则⊙O的半径为( )
 如图,⊙O的弦AB=8,P是劣弧AB中点,连结OP交AB于C,且PC=2,则⊙O的半径为( )
如图,⊙O的弦AB=8,P是劣弧AB中点,连结OP交AB于C,且PC=2,则⊙O的半径为( )| A. | 8 | B. | 4 | C. | 5 | D. | 10 |
 如图所示是由边长都为1的小正方形组成的8×8的正方形网格.若三角形的各个顶点郁在小正方形的顶点上.则这样的图形叫做格点三角形,已知△A0B是格点三角形.
如图所示是由边长都为1的小正方形组成的8×8的正方形网格.若三角形的各个顶点郁在小正方形的顶点上.则这样的图形叫做格点三角形,已知△A0B是格点三角形.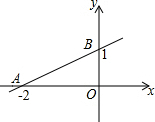 一次函数y=ax+b的图象经过点A、点B,如图所示,则不等式0<ax+b<1的解集是-2<x<0.
一次函数y=ax+b的图象经过点A、点B,如图所示,则不等式0<ax+b<1的解集是-2<x<0.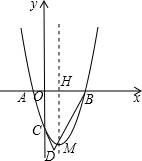 如图,抛物线y=x2+bx+c过点A(-1,0),B(3,0),交y轴于C,对称轴与x轴交于H,顶点为M,AC、BM的延长线交于点D.
如图,抛物线y=x2+bx+c过点A(-1,0),B(3,0),交y轴于C,对称轴与x轴交于H,顶点为M,AC、BM的延长线交于点D.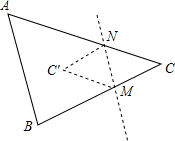 已知,如图,△ABC中,把点C沿直线MN对折得点C′.
已知,如图,△ABC中,把点C沿直线MN对折得点C′. 梯形ABCD中,E为BC上一点,且AE=DE;F为AD上一点,且∠AFB=∠DFC.求证:FMEN为平行四边形.
梯形ABCD中,E为BC上一点,且AE=DE;F为AD上一点,且∠AFB=∠DFC.求证:FMEN为平行四边形.