题目内容
5.设a≠b,m≠n,a,b,m,n是已知数,则方程组$\left\{\begin{array}{l}\frac{x}{a+m}+\frac{y}{b+m}=1\\ \frac{x}{a+n}+\frac{y}{b+n}=1\end{array}\right.$的解是( )| A. | $\left\{\begin{array}{l}x=\frac{(a+m)(a+n)}{a+b}\\ y=\frac{(b+m)(b+n)}{a+b}\end{array}\right.$ | B. | $\left\{\begin{array}{l}x=\frac{(a+m)(b+m)}{a-b}\\ y=\frac{(a+n)(b+n)}{a-b}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}x=\frac{(a+m)(a+n)}{a-b}\\ y=\frac{(b+m)(b+n)}{a-b}\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=\frac{(a+m)(a+n)}{a-b}\\ y=-\frac{(b+m)(b+n)}{a-b}\end{array}\right.$ |
分析 方程组利用加减消元法求出解即可.
解答 解:设a+m=A,b+m=B,a+n=C,b+n=D,
原方程组变形为$\left\{\begin{array}{l}{\frac{x}{A}+\frac{y}{B}=1}\\{\frac{x}{C}+\frac{y}{D}=1}\end{array}\right.$
整理得$\left\{\begin{array}{l}{Bx+Ay=AB①}\\{Dx+Cy=CD②}\end{array}\right.$
①×C-②×A得(BC-AD)x=ABC-ACD,
解得x=$\frac{AC(B-D)}{BC-AD}$,
因为AC(B-D)=(a+m)(a+n)(m-n),BC-AD=(b+m)(a+n)-(a+m)(b+n)=(a-b)(m-n),
所以,x=$\frac{(a+m)(a+n)}{a-b}$;
①×D-②×B得,(AD-BC)y=ABD-CBD,
解得y=$\frac{BD(A-C)}{AD-BC}$,
因为BD(A-C)=(b+m)(b+n)(m-n),AD-BC=(a+m)(b+n)-(b+m)(a+n)=(a-b)(m-n),
所以,y=$\frac{(b+m)(b+n)}{a-b}$,
所以,原方程组的解为$\left\{\begin{array}{l}{x=\frac{(a+m)(a+n)}{a-b}}\\{y=\frac{(b+m)(b+n)}{a-b}}\end{array}\right.$.
故选D.
点评 此题考查了解二元一次方程组,熟练掌握运算法则是解本题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
8. 如图所示,AB∥CD,AD与BC相交于点E,EF是∠BED的平分线,若∠1=30°,∠2=40°,则∠BEF=( )
如图所示,AB∥CD,AD与BC相交于点E,EF是∠BED的平分线,若∠1=30°,∠2=40°,则∠BEF=( )
 如图所示,AB∥CD,AD与BC相交于点E,EF是∠BED的平分线,若∠1=30°,∠2=40°,则∠BEF=( )
如图所示,AB∥CD,AD与BC相交于点E,EF是∠BED的平分线,若∠1=30°,∠2=40°,则∠BEF=( )| A. | 70° | B. | 40° | C. | 35° | D. | 30° |
14.已知⊙O的半径为4cm,直线l与⊙O相切,则圆心O与直线l的距离为( )
| A. | 2cm | B. | 4cm | C. | 8cm | D. | 无法确定 |
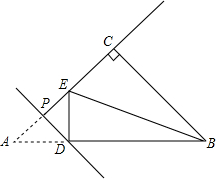 如图,在等腰直角三角形ABC中,∠ACB=90°,AC=3$\sqrt{2}$,点P为线段AC上一个动点,过点P作PD⊥AC交AB于点D,将△APD沿直线PD折叠,点A的对应点为E,连接DE,BE当△DEB的两直角边之比为$\frac{1}{2}$时,AP的长为2$\sqrt{2}$或$\sqrt{2}$.
如图,在等腰直角三角形ABC中,∠ACB=90°,AC=3$\sqrt{2}$,点P为线段AC上一个动点,过点P作PD⊥AC交AB于点D,将△APD沿直线PD折叠,点A的对应点为E,连接DE,BE当△DEB的两直角边之比为$\frac{1}{2}$时,AP的长为2$\sqrt{2}$或$\sqrt{2}$.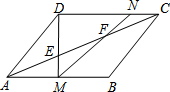 平行四边形ABCD中,AB=28,E、F是对角线AC上的两点,且AE=EF=FC,DE交AB于点M,MF交CD于点N.求AM、CN的长.
平行四边形ABCD中,AB=28,E、F是对角线AC上的两点,且AE=EF=FC,DE交AB于点M,MF交CD于点N.求AM、CN的长.