题目内容
15.抛物线y=ax2+ax-2过直线y=mx-2m+2上的定点A,求抛物线的解析式.分析 先求出定点A,再代入抛物线解析式即可解决.
解答 解:∵直线y=mx-2m+2上的定点A,
∴点A坐标(2,2),
把A(2,2)代入抛物线y=ax2+ax-2得,2=4a+2a-2,
∴a=$\frac{2}{3}$,
∴抛物线解析式为y=$\frac{2}{3}$x2+$\frac{2}{3}$x-2.
点评 本题考查待定系数法确定二次函数解析式,解题的关键是确定定点A的坐标,熟练掌握待定系数法,属于中考常考题型.

练习册系列答案
相关题目
5.设a≠b,m≠n,a,b,m,n是已知数,则方程组$\left\{\begin{array}{l}\frac{x}{a+m}+\frac{y}{b+m}=1\\ \frac{x}{a+n}+\frac{y}{b+n}=1\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}x=\frac{(a+m)(a+n)}{a+b}\\ y=\frac{(b+m)(b+n)}{a+b}\end{array}\right.$ | B. | $\left\{\begin{array}{l}x=\frac{(a+m)(b+m)}{a-b}\\ y=\frac{(a+n)(b+n)}{a-b}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}x=\frac{(a+m)(a+n)}{a-b}\\ y=\frac{(b+m)(b+n)}{a-b}\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=\frac{(a+m)(a+n)}{a-b}\\ y=-\frac{(b+m)(b+n)}{a-b}\end{array}\right.$ |
6.反比例函数y=(2m-1)${x}^{{m}^{2}-1}$,当x>0时,y随x的增大而增大,则m的值是( )
| A. | ±1 | B. | 小于$\frac{1}{2}$的实数 | C. | -1 | D. | 1 |
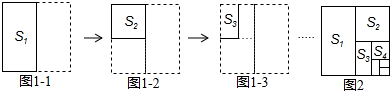
10.将正整数1,2,3,4…按以下方式排列

根据排列规律,从2015到2017的箭头依次为( )

根据排列规律,从2015到2017的箭头依次为( )
| A. | ↓→ | B. | →↓ | C. | ↑→ | D. | →↑ |
20.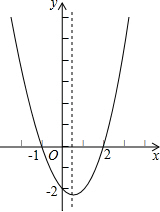 二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
 二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )| A. | 函数有最小值 | B. | 对称轴是直线x=$\frac{1}{2}$ | ||
| C. | 当x<$\frac{1}{2}$时,y随x的增大而减小 | D. | 当-1<x<3时,y>0 |
7.下列计算正确的是( )
| A. | a3÷a=a3 | B. | a+a=2a | C. | (a3)2=a9 | D. | a2•a2=2a2 |
4.下列各组数中,互为相反数的一组是( )
| A. | -2与$\sqrt{(-2)^{2}}$ | B. | -2与$\root{3}{-8}$ | C. | 2与$\sqrt{-4}$ | D. | $\sqrt{1{0}^{-4}}$与2 |
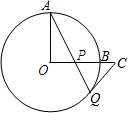 如图,已知⊙O的半径OA⊥OB,过点A的直线交OB于点P,交⊙O于点Q,过Q点引⊙O的切线交OB的延长线于点C,求证:CP=CQ.
如图,已知⊙O的半径OA⊥OB,过点A的直线交OB于点P,交⊙O于点Q,过Q点引⊙O的切线交OB的延长线于点C,求证:CP=CQ.